中学1年数学　比例　確認問題４　解答・解説　

中学1年数学　確認問題4　方程式　解答・解説

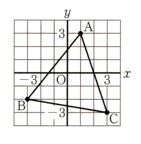
（１）　Ａ（１，３）、Ｂ（−３，−２）、Ｃ（３，−３）を頂点とする

　　　三角形を、図に書いて、その面積を求めてください。ただし、座標の

　　　1目盛りを1ｃｍとします。

    つぎに、三角形の頂点に接する四角形を描きます。

　　まずは、できた四角形の面積を求めます。

　　1目盛りが1ｃｍですから、1辺が6ｃｍの正方形ができます。

　　この。正方形の面積は、(縦)×(横)＝(正方形の面積)

　　　6×6＝36(㎠)　　そこから、外側にできた三角形の面積を求めます。

　　外側にできた三角形は直角三角形ですから、縦、横がわかります。

　　まずは左上の三角形の面積を求めましょう。

　　（Ｑ，Ａ）は4マスですから、4ｃｍ

　　（Ｑ，Ｂ）は5マスですから、5ｃｍ

　　　三角形の面積の求め方は、(底辺)×(高さ)÷2＝三角形の面積

　　　4×5÷2＝10(㎠)

　　　　つぎに、右上の三角形を求めます。

　　（Ａ，Ｐ）は2マスですから、2?

　　（Ｐ，Ｃ）は6マスですから、6cm

　　　2×6÷2＝6(㎠)

　　　　最後に、下の三角形を求めます

　　(R,C)は6マスですから、6cm

　　(B,R)は１マスですから、１cm

　　6×1÷2＝3(㎠)

　　　わかった3つの三角形の合計を四角形から除けば、中の三角形の面積

　がわかります。

　　　△（ABQ）＋△（ACP）＋△（BCR）＝10(㎠)＋6(㎠)＋3(㎠)

　　　　　　　　　　　　　　　　　　　　　　　　＝19(㎠)

　　四角形の面積は、36(㎠)

　　□（CPQR）−△（ABQ）＋△（ACP）＋△（BCR）＝△（ABC）

　　　　□36(㎠)−△19(㎠)＝△17(㎠)

　　　になります。

　　答え　1７(㎠)

（２）ｙ＝ａχのグラフが点（−４，６）を通るとき、ａの値をもとめてく

　　　ださい。

　　　　ｙ＝ａχは、(0,0)を通る直線になります。

　　　　ｙ＝ａχに、(−4,6)を代入してみましょう。

　　　　6＝ａ×(−4)

　　　両辺に(−1/4)をかけます。

　　　　　(−1/4)×6＝ａ×(−4)×(−1/4)
　　
　　　　　　−3/2＝ａ

　　　　比例定数は、−3/2になります。

　　答え　ａ＝−3/2