中学1年数学 立体の表面積と体積 練習問題4 解答・解説
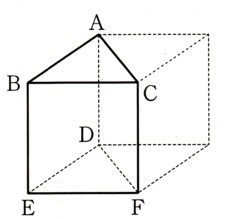
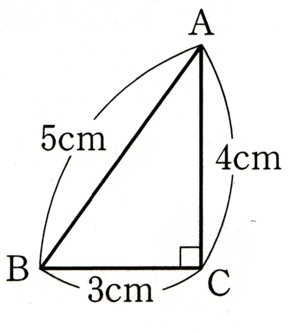
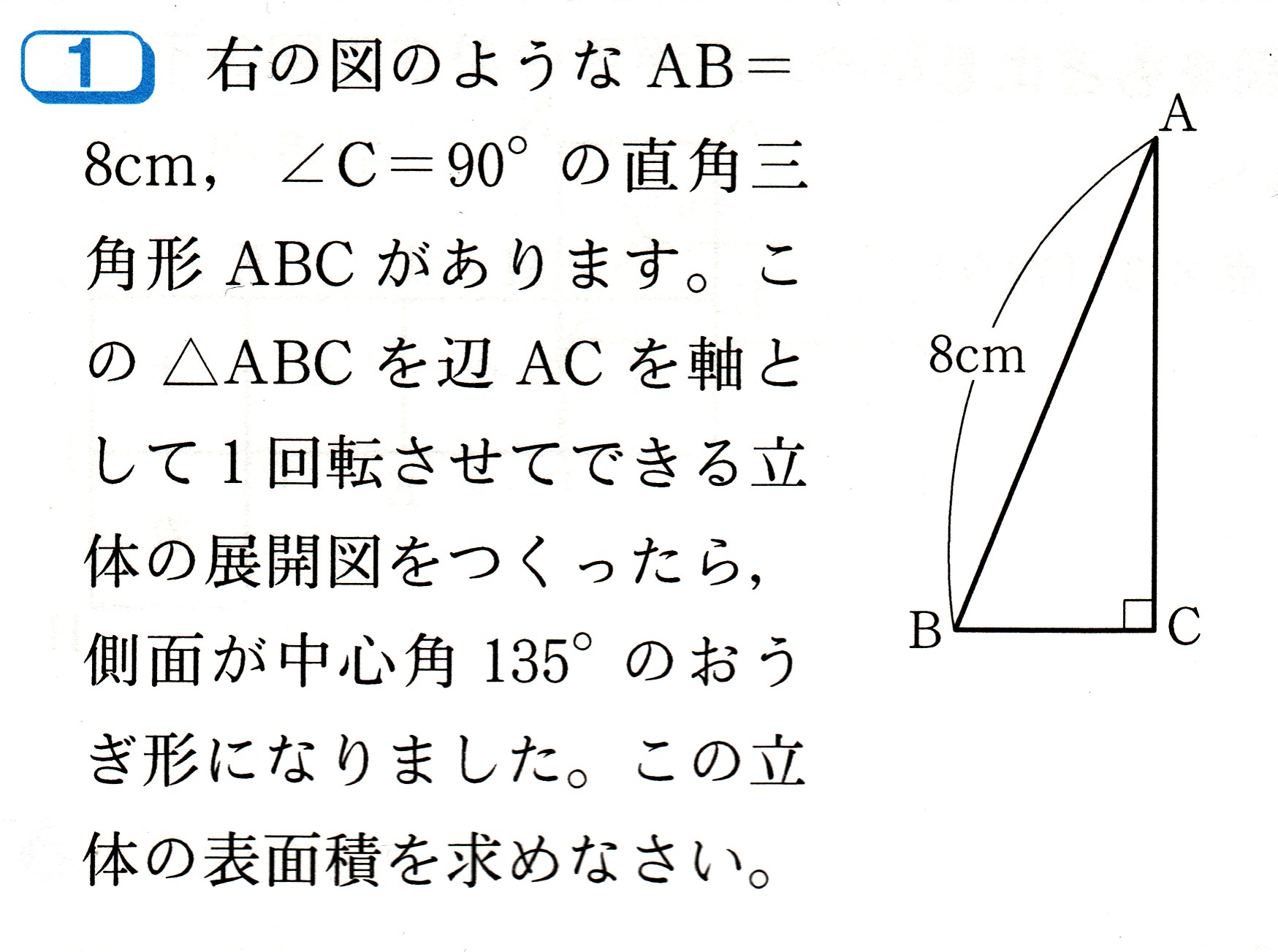
図のような直角三角形ABCを、直線ACを軸として1回転させてできる立体について、
次の問いに答えてください。
(1)表面積を求めてください。
まずは、この直角三角形を回転させると、どのような立体になるかです。
ACを中心に回転させるのですから、できる立体は円錐になります。
円錐の表面積を求める式は
(円錐の表面積)=(底面積)+(側面積)
になります。
まずは、底面積を求めていきます。
底面積は、円になりますから
円の面積を求める式は
(円の面積)=πγ²
半径は、3cm
(円の面積)=(半径)×(半径)×π
=3cm×3cm×π
=9πcm²
次に、側面積を求めます。
側面積は、おうぎ形になりますから
(側面積)=(おうぎ形)
おうぎ形の面積を求める式は
(おうぎ形の面積)=πγ²×中心角/360
このままでは、中心角がわかりませんから。
おうぎ形の弧の長さと、底面の円の周の長さが等しいので
(おうぎ形の弧の長さ)=(底面の円の周の長さ)
それぞれの式は
(2πγ×中心角/360)=(2πγ)
おうぎ形の半径はABの長さになりますから、5cmになります
中心角はわかりませんからχにします。
底面の円の半径は、3cmになります
それでは考えていきましょう。
(2×5cm×π×χ/360)=(2×3×π)
πχ/36=6π
両辺に1/πをかけます
1/π×πχ/36=1/π×6π
次に両辺に36をかけます
36×1/π×πχ/36=1/π×36×6π
χ=216゜
これで中心角がわかりました。
それではおうぎ形の面積を求めましょう。
(おうぎ形の面積)=πγ²×中心角/360
おうぎ形の半径は、5cm
中心角は216゜
(おうぎ形の面積)=(半径)×(半径)×π×中心角/360
=5cm×5cm×π×216/360
=25π×3/5
=15πcm²
(円錐の表面積)=(底面積)+(側面積)
=9πcm²+15πcm²
=24π?²
円錐の表面積がわかりました。
答え 24π?²
(2)体積を求めてください。
円錐の体積を求める式は
V=1/3Sh
(円錐の体積)=1/3×(底面積)×(高さ)
底面積は、(1)で、9πcm²とわかりましたから。
高さです、高さは4cmになっています
(円錐の体積)=1/3×9πcm²×4cm
=12πcm³
答え 12πcm³
(3)直線BCを軸にできた立体は、底面積の半径が4cm、高さが3cmの円錐になります。
(円錐の体積)=1/3×(底面積)×(高さ)
底面積は、円の面積ですから
(円の面積)=πγ²
=(半径)×(半径)×π
=4×4×π
=16π?²
高さは、3cmですから
(円錐の体積)=1/3×16π?²×3cm
=16π?³
になります。
(2)の円錐の体積は12πcm³
(3)の円錐の体積は16πcm³
ですから
(3)−(2)=(体積の差)
16π?³−12π?³=(体積の差)
=4π?³
答え 4π?³









コメント