中学2年数学　1次関数　1次関数の応用　練習問題2・解答

２、グラフの利用

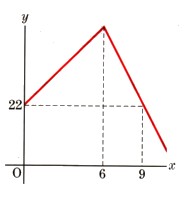
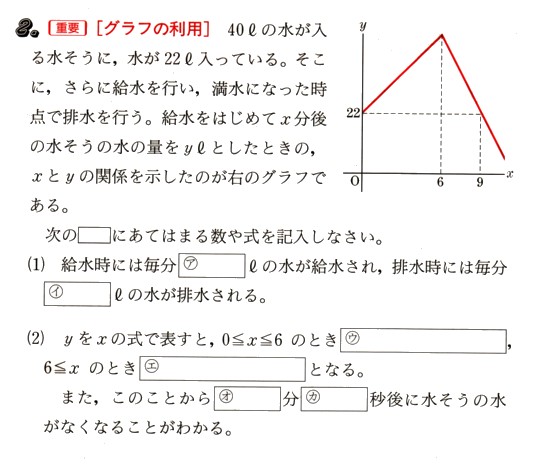
　40ℓの水が入る水槽に、水が22ℓ入っています。そこに、さらに給水を行い、満水になった時点で排水を行います。給水を始めてχ分後の水槽の水の量をｙℓとしたときの、χとワイの関係を示したものが次のグラフになります。

　図　次の［　　］にあてはまる数や式を記入して下さい。

（１）給水時には毎分［ｱ　　］ℓの水が給水され、排水時には毎分［ｲ　］ℓの水が排水されます。

　　右上がりのグラフの頂点部分の座標を考えてみます、

　χ座標は、６になります。

　ｙ座標は、水槽が満水になった時点になりますから、40(ℓ)になります。

　(χ、ｙ)＝(6,40)

　ｙ＝ａχ＋ｂ　の方程式にあてはめてみます。

　(40)＝ａ(6)＋ｂ

　　切片は22ですから

　　40＝6ａ＋22

　　6ａ＋22＝40　

　　6ａ＝40−22

　　6ａ＝18

　　ａ＝3

　　(傾き)＝3

　　傾きは、給水時の毎分の水量になります。

　　給水、毎分3リットル

　　　次の、排水時のグラフを見ていきます。

　(切片)がわかりませんから、２元1次式で考えます。

　　ｙ＝ａχ＋ｂ　の方程式にあてはめてみます。

　　　40＝6ａ＋ｂ
　｛
　　　22＝9ａ＋ｂ

　　　6ａ＋ｂ＝40
　｛
　　　9ａ＋ｂ＝22

　　　6ａ＋ｂ＝40
　−）9ａ＋ｂ＝22　
　　　−3ａ　＝18

　　ａ＝−6

　　ａは、排水時の水量になりますから、毎分6リットルずつ減っていくことがわかります。

　給水時には毎分［ｱ　３　］ℓの水が給水され、排水時には毎分［ｲ　６　］ℓの水が排水されます。

　　答え　ア　3　　、イ　6　

（２）ｙをχの式で表すと、0≦χ≦6　のとき［ｳ　　］、6≦χのとき｢ｴ　｣となります。また、

　　このことから［ｵ　］分[ｶ　]秒後に水槽の水が無くなる事がわかります。

　　χ軸は、時間(分)ということがわかります。

　　０～６(分)までの式は

　　ｙ＝ａχ＋ｂ

　　ｙ＝(傾き)χ＋(切片)

　　(1)で(傾き)は3

　　(切片)は22　とわかりました。

　　ｙ＝3χ＋22

　　(1)で　ａ＝−6　とわかりましたから、

　　40＝6ａ＋ｂ　に　ａ＝−6　を代入します。

　　40＝6(−6)＋ｂ　

　　40＝−36＋ｂ

　　−36＋ｂ＝40

　　ｂ＝40＋36

　　ｂ＝76

　　ｙ＝ａχ＋ｂ

　　ｙ＝(傾き)χ＋(切片)

　　(1)で(傾き)は−6とわかっています。

　　(切片)は、ｂ＝76　ですから、

　　ｙ＝−6χ＋76

　　の式になります。

　　　水の量はｙ　になりますから、

　　ｙに、0を代入します。

　　0＝−6χ＋76

　　−6χ＋76＝0

　　−6χ＝−76

　　　χ＝38/3

             　　 2
　　　χ＝12 ―
            　　 3 (分)

　　　2/3×60＝120/3

　　　　　　＝40(秒)　　　　　　

　　ｙをχの式で表すと、0≦χ≦6　のとき［ｳ　ｙ＝3χ＋22　］、6≦χのとき｢ｴ　ｙ＝−6χ＋76　｣となります。また、

　　このことから［ｵ　12　］分[ｶ　40　]秒後に水槽の水が無くなる事がわかります。

　　
　　　答え　ウ　ｙ＝3χ＋22　、　エ　ｙ＝−6χ＋76　、　オ　12　、　カ　40　