中学２年数学　平面図形　２まとめテスト3・解答

中学２年数学　平面図形　２まとめテスト3・解答

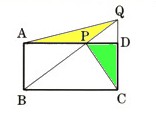
３、長方形ＡＢＣＤの辺ＤＡ上に点Ｐをとり、ＢＰの延長とＣＤとの交点をＱとします。このとき、△ＰＱＡと△ＣＤＰの面積が等しいことを証明してください。

　　
　　この問題は、△ＰＱＡと△ＣＤＰの面積が等しいことを証明しますが、

　　この形のままでは、証明しづらいので少し形を変えて考えていきます。

　　まず考えなければいけないのは、三角形の面積ですから、底辺×高さ÷２の形にしなければならないので、

　　△ＡＱＢを基にして考えていきます。

　　この場合は、底辺をＡＢとしたときに、高さはＢＣになります。

　　つぎに、△ＰＤＣについて考えます。

　　対角線、点Ｄと点Ｂを直線でつなぐと、ＰＤが共通になります。

　　ＡＤとＢＣは長方形ですから平行になります。

　　平行線の性質で、

　　ＡＤ//ＢＣならば、△ＰＤＢ＝△ＰＤＣになります。

　　これで、△ＡＢＤと△ＡＢＱについて考えることができます。

　　△ＡＢＤの面積は底辺ＡＢ、高さＢＣになり、

　　△ＡＢＱ＝ＡＢ×ＢＣ÷２

　　△ＡＢＤ＝ＡＢ×ＢＣ÷２

　　△ＡＢＰは共通ですから

　　残りの、△ＡＱＰと△ＢＰＤは同じ面積になります。

よって、

　　　△ＰＱＡ≡△ＣＤＰ

　になります。