中学2年数学 平面図形 平行四辺形の性質 確認問題6・解答
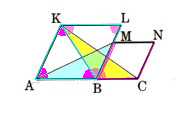
6、 線分AC上に点Bがあります。図のようにひし形KABLとひし形MBCNをつくります。∠KAB=60°とするとき、△ABM≡△KBCであることを証明してください。
線分AC上に点Bがあります。図のようにひし形KABLとひし形MBCNをつくります。∠KAB=60°とするとき、△ABM≡△KBCであることを証明してください。
△ABMと△KBCにおいて
仮定により
ABLKとMBCNは平行四辺形になります。
ゆえに、
AB=KL=AK=BL・・・①
BM=CN=MN=BM・・・②
∠KAB=∠KLB・・・③
∠ABL=∠AKL・・・④
∠CBM=∠CNM・・・⑤
∠BMN=∠BCN・・・⑥
△ABKについて考えます。
辺AK=辺ABは①によりわかっていますから、
二等辺三角形ということがわかります。
仮定により∠AKB=60°ですから、二等辺三角形の底角は残りの120°ということになります。
底角の2つの角は等しくなりますから、120°÷2=60°ということになり
△ABKは正三角形ということがわかりました。
これにより、辺AB=辺KB・・・⑦
△ABKと△LBKは、
①、②より
2つの辺とその間の角がそれぞれ等しくなりますから
△ABK≡△LBK
となります。
合同な三角形の対応する角はそれぞれ等しくなりますから
∠KAB=∠ABK=∠AKB=∠LBK=∠LKB=∠KLB
正三角形ですから、すべての角が60°になります。
∠ABL=∠ABK+∠KBL
∠ABL=60°+60°
∠ABL=120°・・・⑧
∠MBCは、ABKLが平行四辺形ですから、AK//BL
になります。
∠KABと∠MBCは同位角により
∠KAB=∠MBC・・・⑨
∠KBC=∠KBL+∠MBC
∠KBC=60°+60°
∠KBC=120°・・・⑩
∠ABL=∠KBC・・・⑪
②、⑦、⑪より
2つの辺とその間の角がそれぞれ等しくなりますから
△ABM≡△KBC
になります。






コメント