中学1年数学　立体の表面積と体積　確認問題1　解答・解説

中学1年数学　立体の表面積と体積　確認問題1　解答・解説

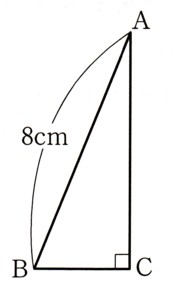
　　図のようなＡＢ＝8ｃｍ、∠Ｃ＝90゜直角三角形ＡＢＣがあります。

　この△ＡＢＣを辺ＡＣを軸として1回転させてできる立体の展開図を

　つくったら、側面が中心角135゜のおうぎ形になりました。この立体

　の表面積を求めてください。

　　この図を一回転してできた立体は、円錐になります。

　　円錐形の展開図は、底面が円になり、

　　　　　　　　　　         　側面がおうぎ形になります。

　　わかっているのは、このおうぎ形の半径は、母線の長さになります

　　から、おうぎ形の半径は8cmになります。

　　　そして、このおうぎ形の中心角が、135゜になります。

　　　(側面の面積)＝(おうぎ形の面積)

　　　(おうぎ形の面積)＝πγ²×中心角／360

　　　　　　　　　　　＝(半径)×(半径)×π×中心角／360

　　　　　　　　　　　＝8cm×8cm×π×135゜／360

　　　　　　　　　　　＝64π×135／360

　　　　　　　　　　　＝24π?²

　　底面の面積を求めるには、半径がわからないといけませんが、

　　このままではわかりません。

　　　そのために、わかる、おうぎ形の弧の長さを求め、この弧の長さ

　　と、底面の円周の長さが同じになりますから。

　　円周の長さがわかります。

　　　円周の長さがわかれば、円周を求める式から、半径を求めます。

　　それでは、おうぎ形の弧の長さを考えましょう。

　　　おうぎ形の弧の長さを求める式は

　　　(おうぎ形の弧の長さ)＝２πγ×中心角／360

　　　　半径は、8cm、中心角は135゜ですから

　　　　　　　　　　　　　＝2×(半径)×π×中心角／360

　　　　　　　　　　　　　＝2×8cm×π×135／360

　　　　　　　　　　　　　＝16π×3/8

　　　　　　　　　　　　　＝6π?

　　　(おうぎ形の弧の長さ)＝(底面の円周)

　　　(おうぎ形の弧の長さ)＝6π?

　　　(底面の円周)＝6π?

　　円周を求める式は

　　　(円周)＝2πγ

　　　　　　＝2×(半径)×π

　　　(円周)は、6π?ですから

　　　　　6π?＝2×(半径)×π　　　

　　　両辺に1/2をかけます

　　　　1/2×6π?＝1/2×2×(半径)×π

　　　両辺に1/πをかけます

　　　　1/π×1/2×6π?＝1/2×2×(半径)×1/π×π

　　　　3＝(半径)

　　　　底面の円の半径が3cmと、わかりました。

　　　これで、底面の円の面積が求められます。

　　　円の面積を求める式は

　　　(円の面積)＝πγ²

　　　　　　　　＝(半径)×(半径)×π

　　　半径は3cmですから

　　　　　　　　＝3cm×3cm×π

　　　　　　　　＝9π?²

　　これで、表面積の側面積と底面積がわかりました。

　　(円錐の表面積)＝(側面積)＋(底面積)

　　　　　　　　　＝(おうぎ形の面積)＋(円の面積)

　　　　　　　　　＝24π?²＋9π?²

　　　　　　　　　＝33π?²

　　　答え　33π?²