中学3年数学 式の展開と因数分解 因数分解 練習問題11・解答
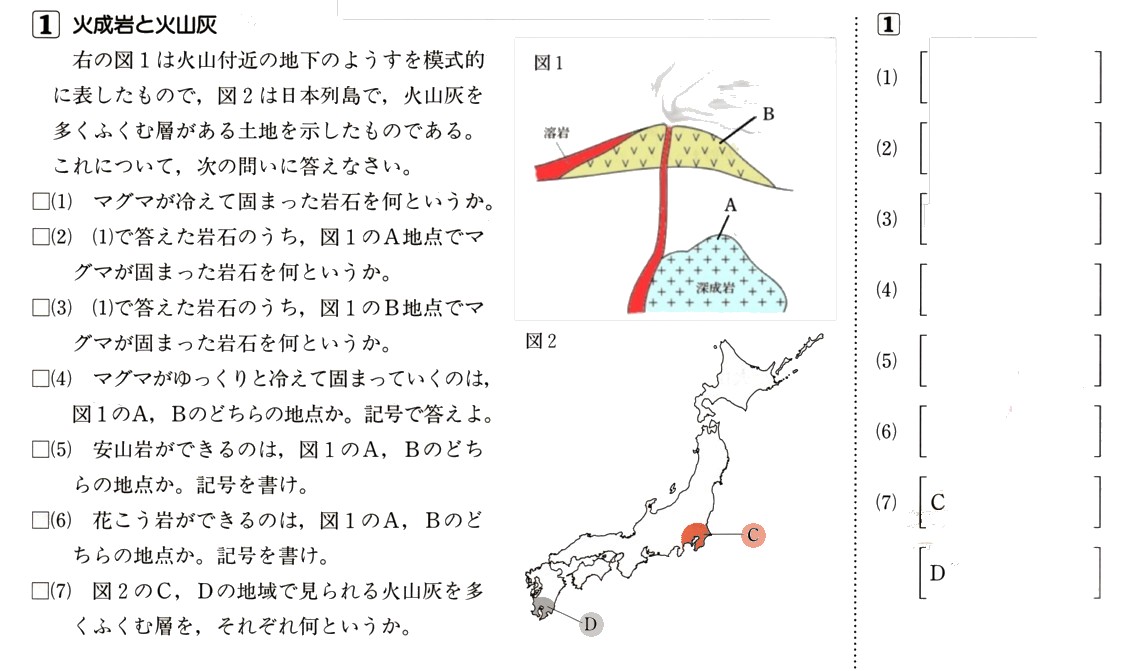
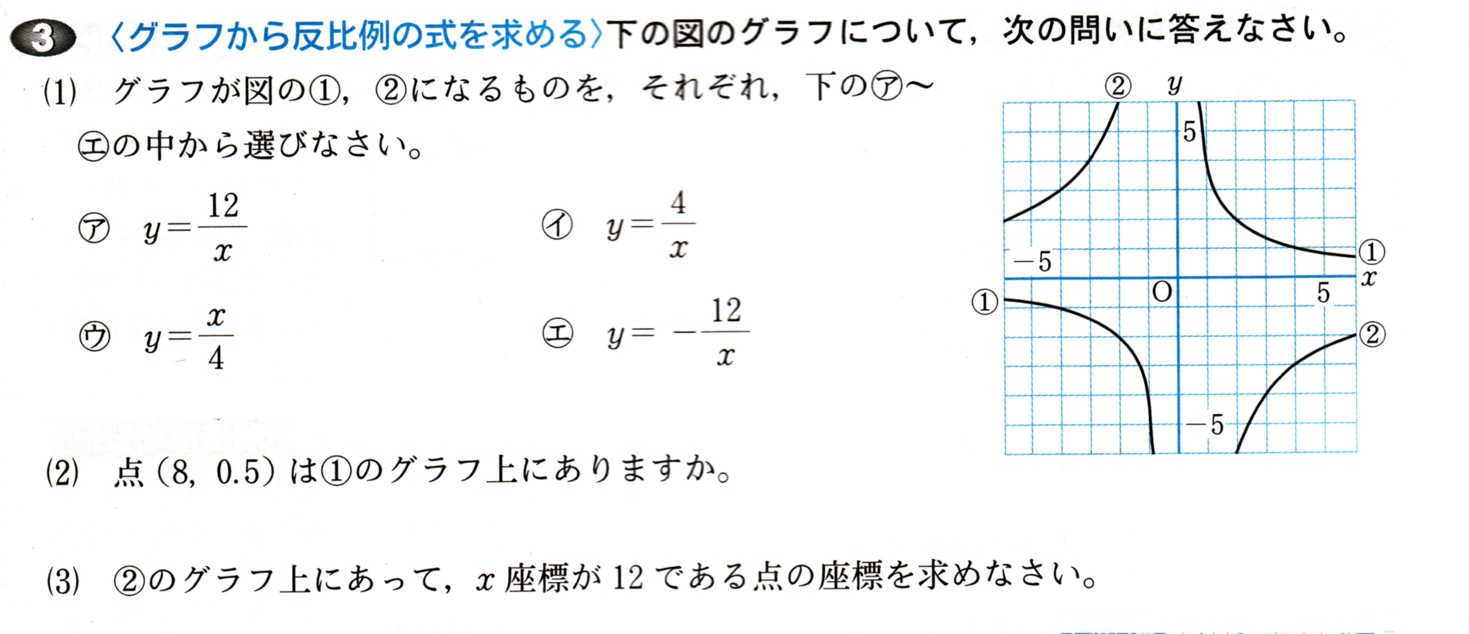
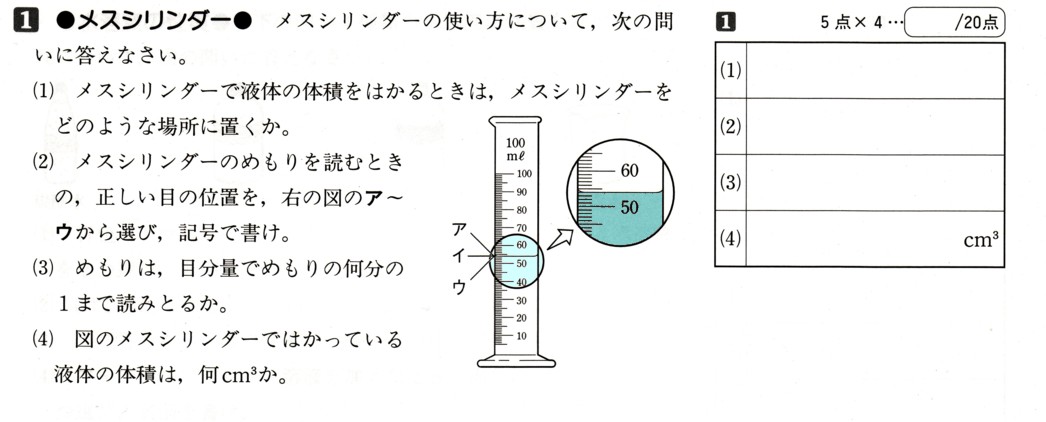
11、次の式を因数分解してください。
今回はいろいろな乗法公式を使って考えていきましょう。
●χ²+(a+b)χ+ab=(χ+a)(χ+b)
●a²+2ab+b²=(a+b)²
●a²−2ab+b²=(a−b)²
●a²−b²=(a+b)(a−b)
を利用します。
ただし、最初に共通因数があるのかを確かめましょう。
①,27−3a²
まずは、共通因数を見つけます。
共通因数は3になります。
ですから、
27−3a²=3(9−a²)
になります。
つぎに、(9−a²)を考えます。
●a²−b²=(a+b)(a−b)
この乗法公式が使えます。
ただし、9を3²の形に変えます。
(3²−a²)=(3+a)(3−a)
となり、3(9−a²)=3(3+a)(3−a)
となります。
答え 3(3+a)(3−a)
②,2χ³−10χ²−12χ
共通因数を探します。
2χが共通因数になります。
2χ³−10χ²−12χ=2χ(χ²−5χ−6)
つぎに、この乗法公式を利用します。
●χ²+(a+b)χ+ab=(χ+a)(χ+b)
かけて(−6)、たして(−5)になるのは
(+1)、(−6)になります。
(χ²−5χ−6)=(χ+1)(χ−6)
2χ(χ²−5χ−6)=2χ(χ+1)(χ−6)
になります。
答え 2χ(χ+1)(χ−6)
③,2χ²+18χ+28
共通因数を探します。
共通因数は2になります。
2χ²+18χ+28=2(χ²+9χ+14)
(χ²+9χ+14)について考えます。
つぎに、この乗法公式を利用します。
●χ²+(a+b)χ+ab=(χ+a)(χ+b)
かけて(+14)、たして(+9)になるのは
(+2)、(+7)になります。
(χ²+9χ+14)=(χ+2)(χ+7)
2(χ²+9χ+14)=2(χ+2)(χ+7)
答え 2(χ+2)(χ+7)
④,−3χ²+3χ+18
共通因数を探します。
共通因数は−3になります。
この場合は符号に注意してください。
−3χ²+3χ+18=−3(χ²−χ−6)
となります。
つぎに、(χ²−χ−6)で考えます。
この乗法公式を利用します。
●χ²+(a+b)χ+ab=(χ+a)(χ+b)
かけて(−6)、たして(−1)になるのは
(+2)、(−3)になります。
(χ²−χ−6)=(χ+2)(χ−3)
−3(χ²−χ−6)=−3(χ+2)(χ−3)
答え −3(χ+2)(χ−3)
⑤,4χ²−64
共通因数を探します。
共通因数は4になります。
4χ²−64=4(χ²−16)
次に、この乗法公式を使います。
●a²−b²=(a+b)(a−b)
ただし、この形にしないといけないので、
(χ²−16)を(χ²−4²)にします。
(χ²−4²)=(χ+4)(χ−4)
となり、
4χ²−64=4(χ²−16)=4(χ²−4²)=4(χ+4)(χ−4)
答え 4(χ+4)(χ−4)












コメント