中学3年数学 関数y=ax²の値の変化 2確認問題2
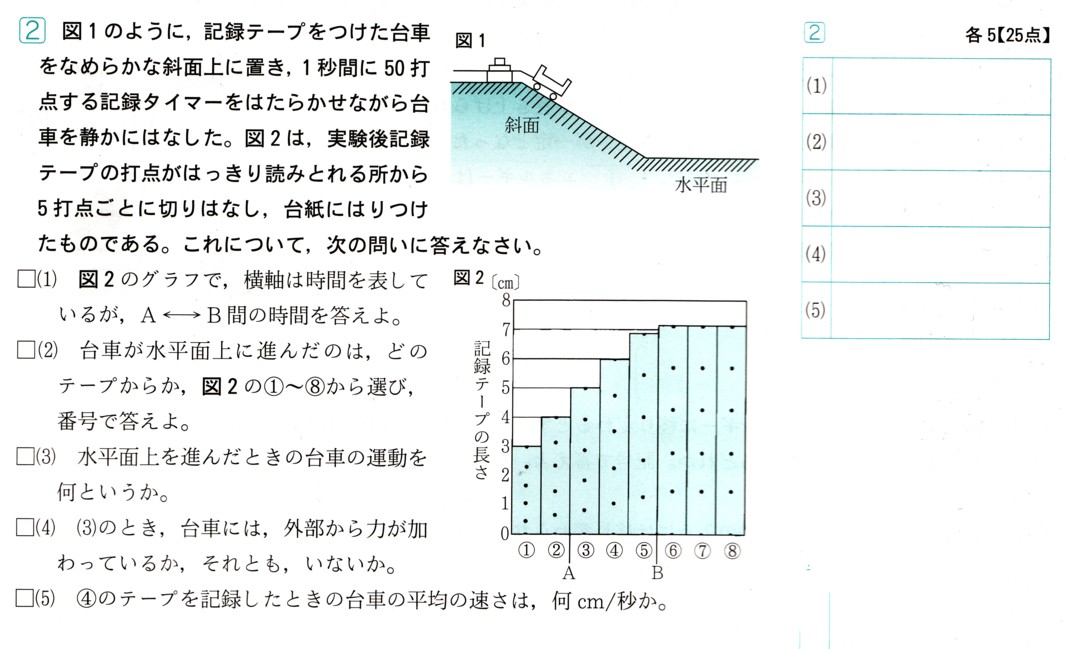
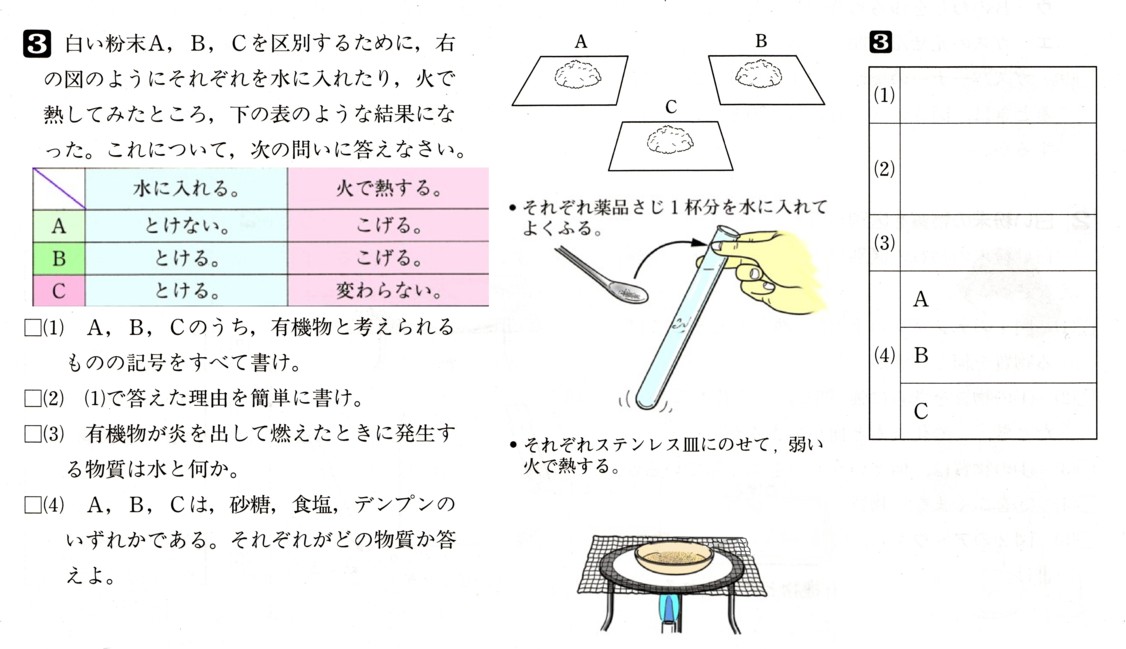
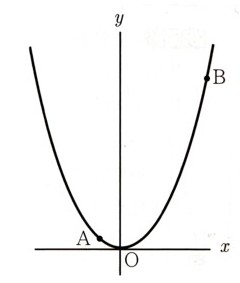
2、次の図 は、関数
は、関数 のグラフになります。このとき、次の問いに答えてください。
(1) x が p から p+2 まで増加するときの変化の割合は5になります。このとき、pの値を求めてください。
yの増加量
変化の割合=――――――
χの増加量
に
、
を代入します。
乗法公式を利用して展開をします。
xの増加量は
yの増加量は
変化の割合は5ですから、
答え 4
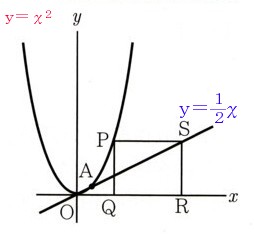
(2)のグラフ上に
、
、
座標が正である
の3点をとります。また、
軸上の正の部分に点
をとります四角形
が平行四辺形になるときの点
、
の座標を求めてください。

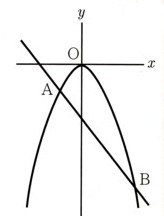
のグラフ上には3点
があり、y軸上には点
があります。
平行四辺形は2つの対角線が中点で交わりますから、点Aと点Bをつなぐ直線の中点を求めます。
、
の半分の位置が中点となります。尚、2点の中点は、x座標、y座標それぞれの距離の平均に位置します。
直線ABの中点の座標は とわかりました。
そして、平行四辺形の対角線は中点で交わりますから、
点C、点Dを結ぶ直線の中点もになります。
点Cの座標は、点Dの座標は
になります。
χ座標
y座標
を代入します。
点Cのy座標はなので、ここに
を代入します。
答え 点Cの座標は、点Dの座標は










コメント