中学3年数学 図形と相似 3確認問題1・解答
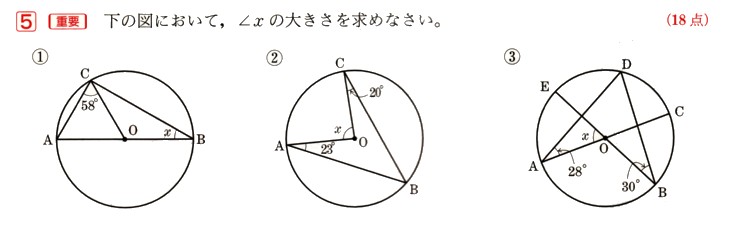
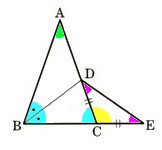
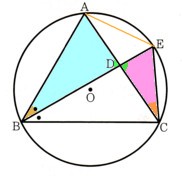
1、図 のように、円Oの周上の点A,B,Cを結んでできる△ABCがあります。
のように、円Oの周上の点A,B,Cを結んでできる△ABCがあります。
∠ABCの二等分線と辺AC、円Oとの交点をそれぞれD,Eとするとき、
次の問いに答えてください。
(1)△DCE∽△DBAであることを証明してください。
答え
[証明]
△DCEと△DBAで、
AEで考えると、∠ABDと∠ACEは弧AEの円周角になります。
∠ABD=∠DCE・・・?
∠ADB=∠EDC(対頂角)・・・?
?,?より
2組の角がそれぞれ等しくなりますから、
△DCE∽△DBA
になります。
(2)△DCEと相似な三角形をもう1つ答えてください。
弧BCで考えます。
∠BACと∠BECは弧BCの円周角になりますから、
∠BAD=∠BEC・・・?
仮定より、
∠ABD=∠EBC・・・?
?,?より
2組の角がそれぞれ等しくなりますから、
△ADB∽△CBE
になります。
よって、△DCE∽△CBE
になります。
答え △CBE
(3)BE=16?,DE=4cmとするとき、CEの長さを求めてください。
△CBE∽△DCEですから、
BE:EC=16:χ
EC:DE=χ:4
になります。
ですから、
16:χ=χ:4
16×4=χ²
64=χ²
χ=±8
EC=8
となります。
答え 8cm








コメント