中学2年数学　1次関数　2元1次方程式とグラフ　練習問題2・解答

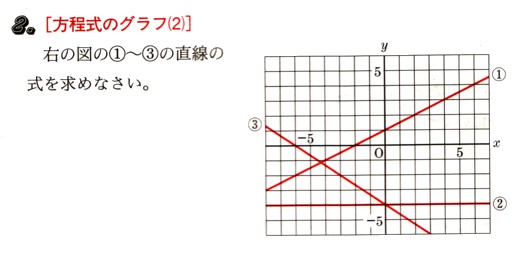
2、方程式のグラフ(2)

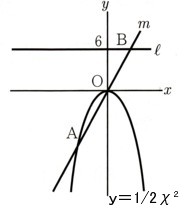
　図の?～?の直線の式を求めてください。

　　ｙ＝ａχ＋ｂ

　　ｙ＝(傾き)χ＋(切片)

　　　　　　　　　　　　　　(ｙの増加量)　　1
　　?　のグラフは、(傾き)＝――――――＝――
　　　　　　　　　　　　　　(χの増加量)　　2

　　　?のグラフの傾きは、右上がりですから、傾きは正の符号になります。

　　(切片)は、ｙ軸に接する点になりますから、(χ、ｙ)＝(0,1)

　　　(切片)＝1　になります。

ｙ＝(傾き)χ＋(切片)

(傾き)＝1/2

(切片)＝1

　　ｙ＝1/2 χ＋1

答え　ｙ＝1/2 χ＋1　　

　　ｙ＝ａχ＋ｂ

　　ｙ＝(傾き)χ＋(切片)

　　　　　　　　　　　　　
　　?　のグラフは、(傾き)　が無くｙ軸に(平行)ですから　
　　　　　　　　　　　　　　
　　　ｙ＝ｂ　の形になります。

　　　正の符号になります。

　　(切片)は、ｙ軸に接する点になりますから、(χ、ｙ)＝(0,−4)

　　　(切片)＝−4　になります。

ｙ＝(切片)

(切片)＝−4

　　ｙ＝−4

答え　ｙ＝−4　

　　ｙ＝ａχ＋ｂ

　　ｙ＝(傾き)χ＋(切片)

　　　　　　　　　　　　　　(ｙの増加量)　　 2
　　?　のグラフは、(傾き)＝――――――＝――
　　　　　　　　　　　　　　(χの増加量)　　3

　　　?のグラフの傾きは、右下がりですから、傾きは負の符号になります。

　　(切片)は、ｙ軸に接する点になりますから、(χ、ｙ)＝(0,−4)

　　　(切片)＝−4　になります。

ｙ＝(傾き)χ＋(切片)

(傾き)＝−2/3

(切片)＝−4

　　ｙ＝−2/3 χ−4

答え　ｙ＝−2/3 χ−4　　