中学２年数学 ２(図形・確率)まとめテスト７・解答
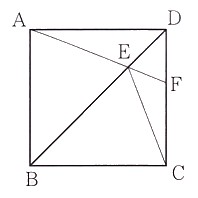
７、図
のように、正方形ＡＢＣＤの対角線ＢＤ上に点Ｅをとり、ＡＥの延長が辺ＣＤとの交わる点をＦとします。
のように、正方形ＡＢＣＤの対角線ＢＤ上に点Ｅをとり、ＡＥの延長が辺ＣＤとの交わる点をＦとします。 このとき、次の問いに答えてください。
（１）∠ＢＣＥ＝∠ＡＦＤであることを証明してください。
答え
〔証明〕
△ＡＥＤと△ＣＥＤにおいて
仮定より
∠ＡＤＥ＝∠ＣＤＥ・・・①（２等分線）
ＡＤ＝ＣＤ・・・②（正方形の各辺はそれぞれ等しい）
ＤＥ＝ＤＥ・・・③（共通）
①，②、③より
２つの辺とその間の角がそれぞれ等しいので
△ＡＥＤ≡△ＣＥＤ
合同な三角形の対応する角はそれぞれ等しくなりますから
∠ＤＡＥ＝∠ＤＣＥ
∠ＤＡＢ＝∠ＤＣＢ（正方形のそれぞれの角は等しい）
∠ＢＡＥ＝∠ＤＡＢー∠ＤＡＥ
∠ＥＣＢ＝∠ＤＣＢ−∠ＤＣＥ
∠ＢＡＥ＝∠ＥＣＢ・・・④
ＡＢ//ＤＣ（正方形）ですから
∠ＢＡＥ＝∠ＤＦＥ（錯角）・・・⑤
④、⑤より
∠ＢＣＥ＝∠ＡＦＤ
になります。
（２）∠ＤＡＦ＝２２°のとき、∠ＢＥＣの大きさを求めてください。
△ＡＢＥと△ＣＢＥにおいて
（１）より∠ＤＡＥ＝∠ＤＣＥですから
∠ＤＡＢ＝∠ＤＣＢ＝９０°（正方形のそれぞれの角は90°）
∠ＥＡＢ＝∠ＤＡＢー∠ＤＡＥ
＝９０°ー２２°
＝６８°
∠ＥＣＢ＝∠ＤＣＢー∠ＤＣＥ
＝９０°ー２２&d
eg;
eg;
＝６８°
∠ＥＡＢ＝∠ＥＣＢ＝６８°・・・①
∠ＥＢＡ＝∠ＥＢＣ・・・②（∠ＡＢＣの二等分線＝４５°＋４５°）
三角形の内角の和は180°ですから
∠ＢＥＣ＝１８０°ー（∠ＥＢＣ＋∠ＥＣＢ）
＝１８０°ー（４５°＋６８°）
＝１８０°ー１１３°
＝６７°
答え ６７°
コメント