中学３年数学 関数ｙ＝ａχ² ２まとめテスト１・解答
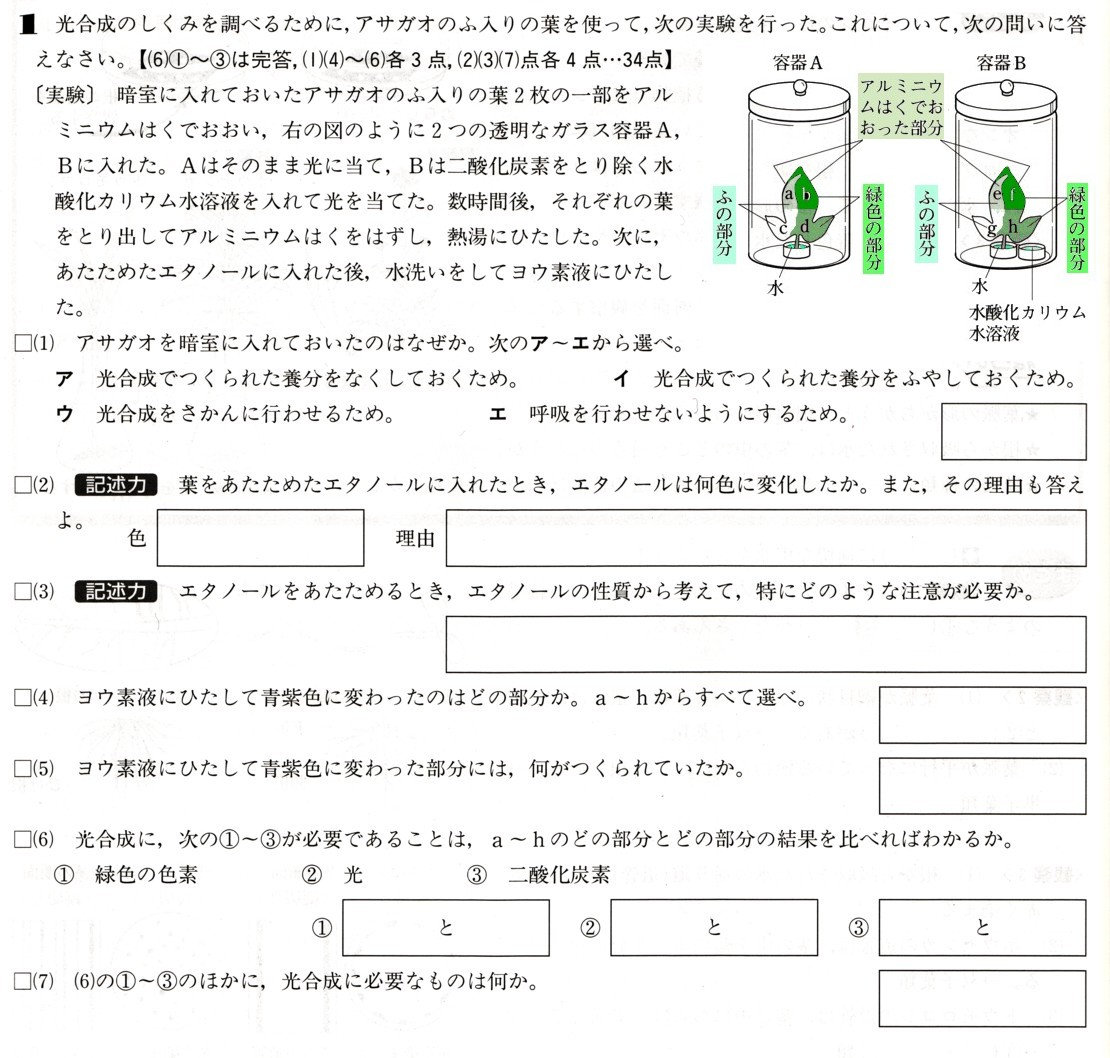
１、図
のように、関数ｙ＝１/２χ²のグラフ上に２点Ａ，Ｂがあります。点Ａはχ座標が−５の点になり、点Ｂはχ座標とｙ座標が等しく、原点と異なる点なります。また、直線ＡＢとｙ軸との交点をＣとします。点Ａからχ軸に垂線ＡＨをひきます。このとき、次の問いに答えてください。
（１）点Ｂの座標を求めてください。
ｙ＝１/２χ²にχ＝ｂ、ｙ＝ｂを代入します。
ｂ＝１/２（ｂ²）
ｂ＝ｂ²/２
２ｂ＝ｂ²
ｂ²−２ｂ＝０
ｂ（ｂ−２）＝０
Ａ×Ｂ＝０ならばＡ＝０またはＢ＝０になります。
ｂ＝０、ｂ−２＝０
ｂ＝２
ｂは原点と異なる点ですからｂ＝２になります。
これにより、点Ｂの座標は
点Ｂの座標（２、２）になります。
答え （２，２）
（２）直線ＡＢの式を求めてください。
点Ａのχ座標は−５ですから、
ｙ＝１/２χ²にχ＝−５を代入します。
ｙ＝１/２（−５²）
ｙ＝２５×１/２
ｙ＝２５/２
点Ａの座標は（−５、２５/２）
直線ＡＢの式は右下がりになりますから、ｙ＝−ａχ＋ｂになります。
ｙ＝−ａχ＋ｂにＡ（−５、２５/２）、Ｂ（２，２）を代入します。
２５/２＝−ａ（−５）＋ｂ
｛
２＝−ａ（２）＋ｂ
２５/２＝５ａ＋ｂ
｛
４/２＝−２ａ＋ｂ
２５/２＝５ａ＋ｂ
−）４/２＝−２ａ＋ｂ
２１/２＝７ａ
７ａ＝２１/２
１４ａ＝２１
ａ＝２１/１４
ａ＝３/２
２５/２＝５ａ＋ｂにａ＝３/２を代入します。
２５/２＝５×（３/２）＋ｂ
２５/２＝１５/２＋ｂ
ｂ＝２５/２−１５/２
ｂ＝１０/２
ｂ＝５
傾きは３/２、切片は５になります。
この直線の式は
ｙ＝−３/２χ＋５
になります。
答え ｙ＝-３/２χ＋５
（３）ｙ軸を軸として、台形ＡＨＯＣを１回転させてできる立体の体積を求めてください。
できる図形は円柱から三角錐を除いた立体になります。
（円柱）−（三角錐）＝（この立体の体積）
まずは、円柱の体積を考えます。
底面＝半径×半径×π
半径はＯＨの長さになりますから５
５²π＝２５π・・・?
高さはＡＨの長さになりますから。
２５/２
円柱の体積は２５π×２５/２＝６２５π/２
次に、三角錐の体積を考えます。
底面の面積は?とおなじですから
５²π＝２５π・・・?
高さは点Ａのｙ座標から直線ＡＢの切片５を引けば高さがわかります。
２５/２−５＝２５/２−１０/２＝１５/２
三角錐の体積は
２５π×１５/２×１/３＝３７５π/６＝１２５π/２
６２５π/２−１２５π/２＝５００π/２＝２５０π
答え ２５０π
コメント