中学2年数学 確率 場合の数 確認問題2・解答
2、大小2個のさいころを投げるとき,次の問いに答えてください。
(1)目の出方は,全部で何通りになるか答えてください。
さいころは1~6までありますから、6通りあります。
さいころが大小2つありますから、
大きいさいころの目の出る場合の数×小さいさいころの目の出る場合の数=2つのさいころの目の出る場合の数(通り)
6(通り)×6(通り)=36(通り)
答え 36(通り)
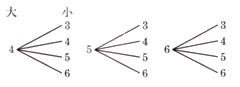
(2)大きいさいころの目の数が4以上で,小さいさいころの目の数が3以上である目の出方は何通りになるか答えてください。

4以上は4,5,6になり、
3以上は3,4,5,6になります。
(大きいさいころ)×(小さいさいころ)=(何通りか)
3(通り)×4(通り)=12(通り)
答え 12(通り)
(3)2つのさいころの目の数の和が奇数である目の出方は何通りか答えてください。
表にしてみるほうがわかりやすくなります。

答え 18(通り)
(4)少なくとも1つのさいころの目の数が1である目の出方は何通りになるか答えてください。
2つのさいころの目が共に1でないような目の出方は、
5×5=25(通り)
ですから、少なくとも1つのさいころの目の数が1であるような目の出方は、
(2つのさいころの目の出る場合の数)−(2つのさいころが1でない場合の数)=(1が出る場合の数)
36(通り)−25(通り)=11(通り)
(1,1)、(1,2)、(1,3)、(1,4)、
(1,5)、(1,6)、(2,1)、(3,1)、
(4,1)、(5,1)、(6,1)
答え 11(通り)







コメント