中学2年数学 連立方程式 連立方程式の応用 練習問題2・解答
2,距離・速さ・時間の問題
「50キロメートルの道のりを自転車で走りました。はじめ時速15kmで走り、途中から時速10kmで走ったら、全部で4時間掛かりました。時速15kmで走った距離を求めてください。」
この問題を次のように解きました。[ ]にあてはまるものを答えてください。
道のり全体の距離は、50kmになりますから。時速15kmで走った距離はχ?、時速10kmで走った距離をy?になりますから、
χ(?)+y(?)=50(?)
となります。
時速15kmで走った距離をχ?、時速10kmで走った距離をy?とすると、道のりの関係より、[ア χ+y ]=50 ・・・?
時間の関係で考えると、
時間=距離÷速さ ですから
時速15kmで走った時間は、χ(?)÷15(?)
時速10kmで走った時間は、y(?)÷10(?)
になります。
全部で4時間掛かったのですから、
(χ/15)+(y/10)=4(時間)
になります。
時間の関係より、χ/15+[イ y/10 ]=[ウ 4 ] ・・・?
χ(?)+y(?)=50
{
(χ/15)+(y/10)=4(時間)
y=50−χ
(χ/15)+(y/10)=4(時間) に y=50−χ を 代入します。
χ/15+(50−χ)/10=4
両辺に30を掛けます。
30(χ/15)+30(y/10)=4×30
2χ+3(50−χ)=120
2χ+150−3χ=120
−3χ+2χ=120−150
−χ=−30
χ=30
y=50−χ に χ=30 を代入します。
y=50−30
y=20
?,?を連立方程式として解くと、χ=[エ 30 ]、y=[オ 20 ]
求めるのは時速15kmで走った距離ですから、答えは、[カ 30 ]?。
答え ア、χ+y イ、y/10 ウ、4 エ、30 オ、20 カ、30




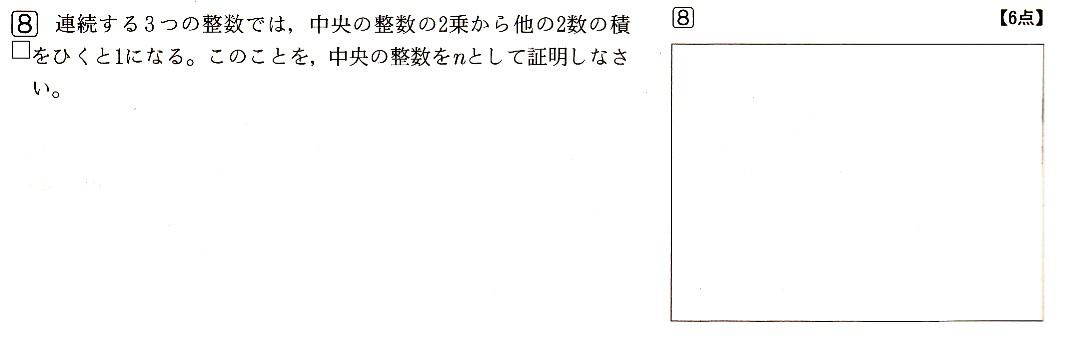



コメント