中学2年数学 確率 場合の数 確認問題3・解答
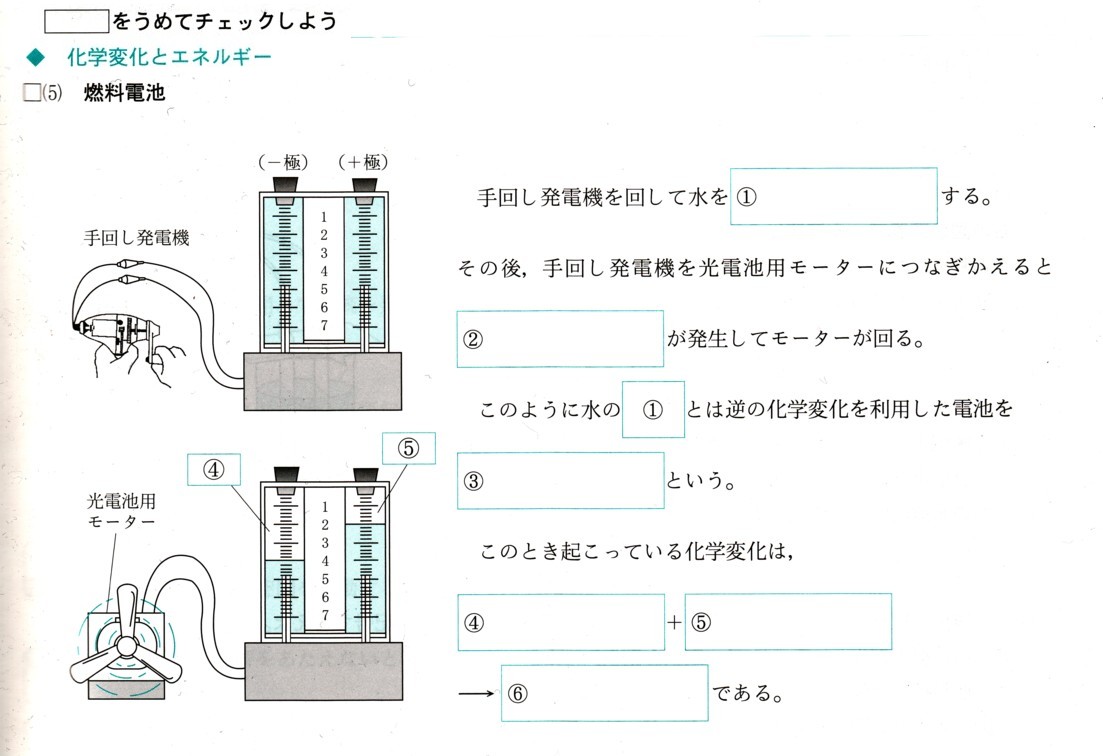
3、2人の男子と2人の女子が1列に並ぶとき,次の問いに答えてください。
(1)全部で何通りの並び方がありますか?答えてください。
全部で4人の男女がいますから、
① 最初の列には4通り
② 2列目には3通り
③ 3列目には2通り
④ 4列目は残った1人になります。
樹形図をかいてみましょう。
男子はA,Bとし、女子はA’、B’とします。

4×3×2×1=24(通り)
答え 24(通り)
(2)両端に女子がいる並び方は何通りになりますか?
男子をAとしたとき、もう一人の男子をBとします。
女子をA’としたとき、もう一人の女子をB’とします。
(A’−A−B−B’)、(A’−B−A−B’)、
(B’−A−B−A’)、(B’−B−A−A’)、
になります。

両端に女子がくる並び方は2通りあり、内側の2列に男子がきます、その場合の数は2通りになりますから、
(両端に女子がくる場合の数)×(内側に男子がくる場合の数)=(両端に女子がくる場合の数)
2(通り)×2(通り)=4(通り)
答え 4(通り)
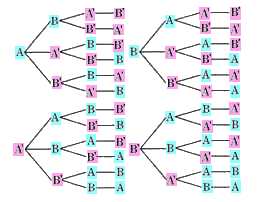
(3)2人の女子が隣会って
いる並び方は何通りありますか?
いる並び方は何通りありますか?
隣り合っているのですから、2人の女子を1人として考えても同じになります。
そうすると、
1列目は3(通り)あり
2列目は2(通り)になり
3列目は残りの1人になります。
(1列目)×(2列目)×(3列目)=(3人の並ぶ列の場合の数)
3×2×1=6(通り)
そして、2人の女子が入れ代わった場合の数は
(1人目の女子)×(もう1人の女子)=(女子が入れ代わった場合の数)
(2)×(1)=(2)

男子をA、B
女子をA’、B’ とします。
(A’B’AB)、(A’B’BA)、(B’A’BA)、
(B’A’AB)、(BAA’B’)、(ABA’B’)、
(ABB’A’)、(BAB’A’)、(BB’A’A)、
(BA’B’A)、(AA’B’B)、(AB’A’B)、
になります。
答え 12(通り)











コメント