中学2年数学 1次関数 1次関数の応用 練習問題1・解答
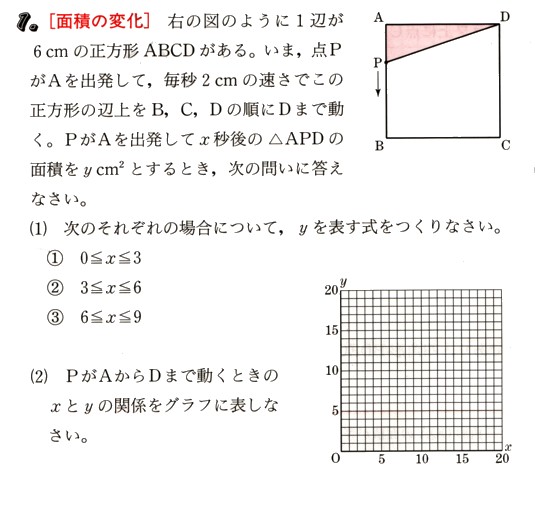
1、図 のように1辺が6cmの正方形ABCDがあります。今、点PがAを出発して、毎秒2cmの速さでこの正方形の辺上をB,C,Dの順にDまで動きます。PがAを出発してχ秒後の△APDの面積をy㎠とするとき、次の問いに答えて下さい。
のように1辺が6cmの正方形ABCDがあります。今、点PがAを出発して、毎秒2cmの速さでこの正方形の辺上をB,C,Dの順にDまで動きます。PがAを出発してχ秒後の△APDの面積をy㎠とするとき、次の問いに答えて下さい。
(1)次のそれぞれの場合について、yを表す式をつくって下さい。
? 0≦χ≦3
点Pは,毎秒2cm進みますから、1辺を3秒かかります。
χは、χがかかる時間ですから、0~3秒の間は、辺AB間の移動になります。
この四角形のAD(6cm)を△ADPの(底辺)=6cmと考えます。
△ADPの(高さ)は、APになります。
三角形の面積の求める式は
(面積)=(底辺)×(高さ)÷2
yが、面積になり、χが高さになります。
(高さ)=距離になります。
(距離)=(速さ)×(時間)
=(毎秒2cm)×(χ)秒
(面積)={(毎秒2cm)×(χ)秒}×1/2
y=6(?)×2χ×1/2
y=6χ
答え y=6χ
? 3≦χ≦6
χの変域が3~6ということは、辺BCをB→Cに移動するということになります。
点Dを中点に点Pはを移動するということは、三角形の形は変わりますが、三角形の(底辺)を辺BCと考えると、(底辺)と(高さ)は同じになりますから、面積は同じになります。
面積=(底辺)×(高さ)÷2
y=6×6×1/2
y=18
答え y=18
? 6≦χ≦9
χが6秒~9秒の点Pの移動は、辺CDの移動になります。
点PがC→Dに向かうと三角形の面積はだんだん小さくなります。
この場合は底辺を辺ADにしていますから、高さが短くなっていきます。
時間がたつと短くなります。ただし、注意しないといけないのは、
点Pは、A→B→C→Dと移動します、
変域が6≦χ≦9ですから、A→Dの移動距離は18cm進んだことになります。
点Pは秒速2cmで進みますから2χ(?)
時間が進むごとに距離は18?から減っていきますから
18−2χ=(CD間を進んだ距離)
考え方を変えてみると、点PがD→Cに進んだと考えることができます。
三角形の面積=(底辺)×(高さ)÷2
=辺(AD)×(CD間を進んだ距離)÷2
=6(?)×(18−2χ)÷2
=54−6χ
答え y=−6χ+54
(2)PがAからDまで動くときのχyの関係をグラフに表して下さい。
0≦χ≦3 を y=6χ の式にあてはめてみます。(切片)がありませんから原点Oから始まります。
(yの増加量) 6
(傾き)は6ですから、――――――=――
(χの増加量) 1
つぎに、3≦χ≦6 は y=18で一定ですから、χ軸に平行になります。
6≦χ≦9 を y=−6χ+54 の式にあてはめてみます、
(切片)は54ですが、今回は3≦χ≦6 の続きで考えます。、
(傾き)が−6ですから、符号が(−)で







コメント