中学２年数学 平面図形 平行四辺形の性質 確認問題８・解答
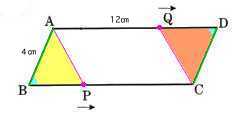
８、
ＡＢ＝４?、ＡＤ＝12?の平行四辺形の辺上を、点Ｐは毎秒0.2?の速さでＡからＢを経てＣまで進み、点Ｑは毎秒0.3?の速さでＡからＤを経てＣまで進むものとします。Ｐ、ＱがＡを同時に出発してから何秒後に、△ＡＢＰと△ＣＤＱが合同になるか答えてください。
まずは、合同な三角形を考えてみます。
合同な三角形になるには、
ＡＢＣＤは平行四辺形ですから
向かい合う２つの辺はそれぞれ等しくなります。
それにより、
ＡＢ＝ＣＤ
となります。
つぎに、２つの対角はそれぞれ等しくなりますから
∠Ｂ＝∠Ｄ
ということになり
辺ＢＰと辺ＱＤが等しければ△ＡＢＰと△ＣＤＱとなります。
点ＰはＢＣ上にありますから４?以上は進まないといけません。
点Ｐは毎秒0.2?進みますから、ＢＰの距離はＡＰの距離からＡＢの距離を引いた長さになります。
（距離）＝（速さ）×（時間）
ＢＰ? ＝ （0.2 × χ）ーＡＢ
ＡＢは４?ですから
ＢＰ＝χ／５ー４
になります。
つぎに、ＱＤは、ＡＤからＡＱの長さを引いた長さになります。
ＡＤは12?ですから、
ＱＤ＝12?ー（0.3×χ）
ＢＰ＝ＱＤにならないといけないのですから連立方程式にします。
χ／５ー４＝12ー（3／１０×χ）
両辺に10をかけます。
２χー４０＝１２０ー３χ
２χ＋3χ＝120＋40
５χ＝160
χ＝32
χは時間ですから32秒後になります。
答え 32秒後
コメント