中学2年数学 平面図形 平行四辺形の性質 確認問題2・解答
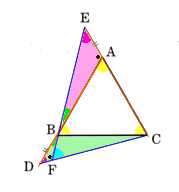
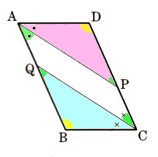
2、図 のように、平行四辺形ABCDの∠A、∠Cの二等分線を引き、辺CD、ABとの交点をそれぞれP、Qとします。このとき、AQ=CPであることを証明してください。
のように、平行四辺形ABCDの∠A、∠Cの二等分線を引き、辺CD、ABとの交点をそれぞれP、Qとします。このとき、AQ=CPであることを証明してください。
「解説」
△ADPと△BCQにおいて
仮定により
ABCDは平行四辺形ですから、
2つの対角は等しくなりますから、
∠D=∠B・・・①
ABCDは平行四辺形は、向かい合う2つの辺はそれぞれ等しくなりますから。
AD=BC・・・②
ABCDは平行四辺形ですから、
2つの対角は等しくなりますから、
∠A=∠C
●●は、∠A、××は、∠Cになり、
∠A=●●
∠C=××
●=∠A×1/2
×=∠C×1/2
ですから、
●=×・・・③
になります。
①、②、③より
1つの辺とその両端の角がそれぞれ等しくなりますから
△ADP≡△BCQ
になります。
合同な三角形の対応する角はそれぞれ等しくなりますから
∠APD=∠BQC・・・④
になります。
④より、
∠AQC=180ー∠BQC
∠CPA=180ー∠APD
ですから、
∠AQC=∠CPA・・・⑤
③、⑤より
2つの対角がそれぞれ等しくなりますから
四角形AQCPは平行四辺形になります。
答え
〔証明〕
△APDと△CQBにおいて
四角形ABCDが平行四辺形であることから、
AD=CB・・・①
∠PDA=∠QBC・・・②
さらに、仮定より、
∠DAP=1/2∠A
∠BCQ=1/2∠C
∠A=∠Cであることから
∠DAP=∠BCQ・・・③
①、②、③より
1辺とその間の角がそれぞれ等しいので、
△APD≡△CQB
よって、DP=BQ・・・④
ここで、AB=CDであることから、④より
AQ=CP








コメント