中学2年数学 円周角の定理 練習問題４・解答
４、円周角と中心角
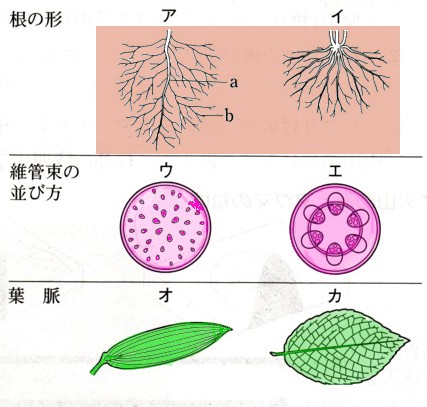
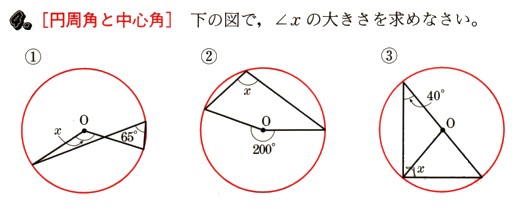
図で、∠χの大きさを求めてください。
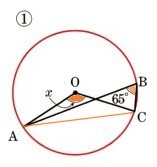
① 
弧ＡＣにおいて、
弧ＡＣにおいて、 ∠ＡＢＣは、円周角になります。
∠ＡＢＣ＝65°
∠ＡＯＣは、弧ＡＣの中心角になりますから、
弧ＡＣの円周角65°の２倍の角度になります。
∠ＡＯＣ＝65°×２
＝130°
答え χ＝130°
② 
弧ＢＣにより、
弧ＢＣにより、 χは、弧ＢＣの円周角になります。
＊この問題には注意してください。
弧ＢＣの中心角は、200°になります。
ですから、円周角は中心角の半分になりますから、
∠ＢＡＣ＝200°×１／２
＝100°
答え χ＝100°
③ 
△ＢＯＣで考えます。
△ＢＯＣで考えます。 ＢＯと、ＣＯは、円の半径になりますから、
ＢＯ＝ＣＯ
になり、
△ＢＯＣは、二等辺三角形になります。
二等辺三角形ですから２つの底角は等しくなります。
この、２つの底角の和は△ＡＯＢの頂角になります。
△ＡＯＢは、ＯＡ、ＯＢが円の半径になりますから、
ＯＡ＝ＯＢ
ですから、二等辺三角形になりますから、２つの底角は等しくなります。
∠ＯＡＢ＝40°ですから、
∠ＯＢＡ＝40°になります。
三角形の内角の和は180°ですから、
頂角∠ＡＯＢ＝180°ー（40°＋40°）
＝180°ー80°
＝100°・・・①
①より
△ＯＢＣの２つの底角の和の外角が100°とわかりましたから、
△ＯＢＣは二等辺三角形ですから、２で割れば１つの底角の角度がわかります。
χは、底角の１つになりますから、
100÷2＝50°
∠ＯＢＣ＝50°
答え χ＝50°
コメント