中学2年数学 平面図形 平行線と面積 確認問題4・解答
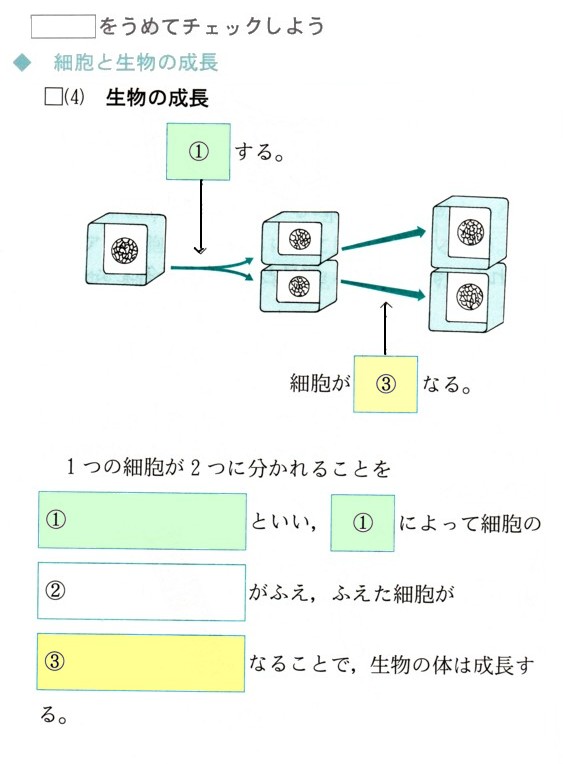
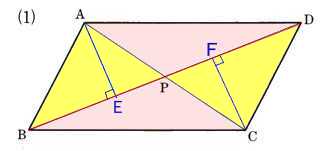
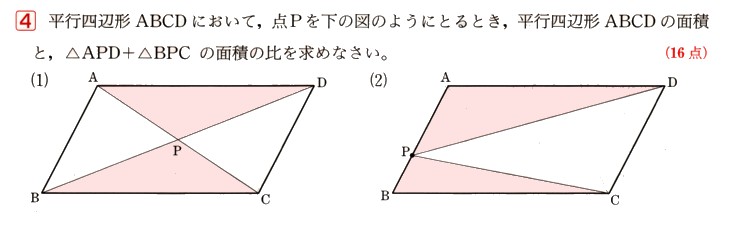
4、平行四辺形ABCDにおいて、点Pを図 のようにするとき、平行四辺形ABCDの面積と、△APD+△BPCの面積の比を求めてください。
のようにするとき、平行四辺形ABCDの面積と、△APD+△BPCの面積の比を求めてください。
 のようにするとき、平行四辺形ABCDの面積と、△APD+△BPCの面積の比を求めてください。
のようにするとき、平行四辺形ABCDの面積と、△APD+△BPCの面積の比を求めてください。(1)△APBと△APDにおいて
ABCDは平行四辺形で、BD、ACの2直線は対角線になります。
対角線の交点はそれぞれの直線の中点で交わりますから、
BPとDPは同じ長さになります。
BP=DP・・・①
BDから点Aに垂線を引きます、BDに交わる点をEとします。
三角形の面積は、
(底辺)×(高さ)÷2ですから
△ABP=BP×AE÷2・・・②
△ADP=PD×AE÷2・・・③
②、③より
△ABP≡△ADP
同じように△BPCと△DPCにおいて
BDから点Cに垂線を引きます、BDに交わる点をFとします。
△BPC=BP×CF÷2・・・④
△DPC=DP×CF÷2・・・⑤
④、⑤より
△BPC≡△DPC
△ABP=△ADP=△BPC=△DPC
ということになります。
△を1と考えると
平行四辺形ABCD=△ABP+△ADP+△BPC+△DPC は、
=1+1+1+1
=4
△APD+△BPC=1+1
=2
平行四辺形ABCD:△APD+△BPC=4:2
=2:1
答え 2:1
(2)△APDと△BPCの面積は、(底辺)×(高さ)÷2ですから
点DからABの延長線上に垂線Eをつくります。
 そうすると、この直線DEは△APDと△BPCの共通の高さになります。
そうすると、この直線DEは△APDと△BPCの共通の高さになります。底辺になるAPとBPの長さは辺ABですから
AP+BP=AB
になります。
そうすると、
△APD+△BPCの面積と△ABDの面積は底辺、高さが同じ三角形の面積になります。
△APD+△BPC=△ABD
ですから、△ABDの面積で考えます。

辺BDは平行四辺形BDの対角線になりますから、
△ABDと△CBDは等しい三角形になりますから
平行四辺形ABCD=△ABD+△CBD
△ABDを1とすると、
平行四辺形=1+1
=2
△ABD=1
平行四辺形:△ABD=2:1
平行四辺形:△APD+







コメント