中学3年数学 式の展開と因数分解 多項式の計算 2確認問題2・解答
2,次の式を展開してください。
●(χ+a)(χ+b)=χ²+(a+b)χ+ab
①,(7χ+1/3)(7χ+2/3)
=(7χ)²+(1/3+2/3)7χ+1/3×2/3
=49χ²+7χ+2/9
答え 49χ²+7χ+2/9
②,(3/4a+2b)(3/4aー3b)
=(3/4a)²+(2bー3b)3/4a+2b×(−3b)
=9/16a²ー3/4abー6b²
答え 9/16a²ー3/4abー6b²
●(a+b)²=a²+2ab+b²
●(a−b)²=a²ー2ab+b²
③,(1/3χ+9)²
=(1/3χ)²+2(3χ)+81
=1/9χ²+6χ+81
答え 1/9χ²+6χ+81
④,(3/4χー2/3y)²
=(3/4χ)²−2(3/4χ×2/3y)+(2/3y)²
=9/16χ²ー2(6/12χy)+4/9y²
=9/16χ²ーχy+4/9y²
答え 9/16χ²ーχy+4/9y²
●(a+b)(a−b)=a²−b²
⑤,(5y+2/3)(5yー2/3)
=(5y)²ー(2/3)²
=25y²ー4/9
<
br />
答え 25y²ー4/9
⑥,(ー1/4χ+8y)(ー1/4χー8y)
=(ー1/4χ)²ー(8y)²
=1/16χ²ー64y²
答え 1/16χ²ー64y²








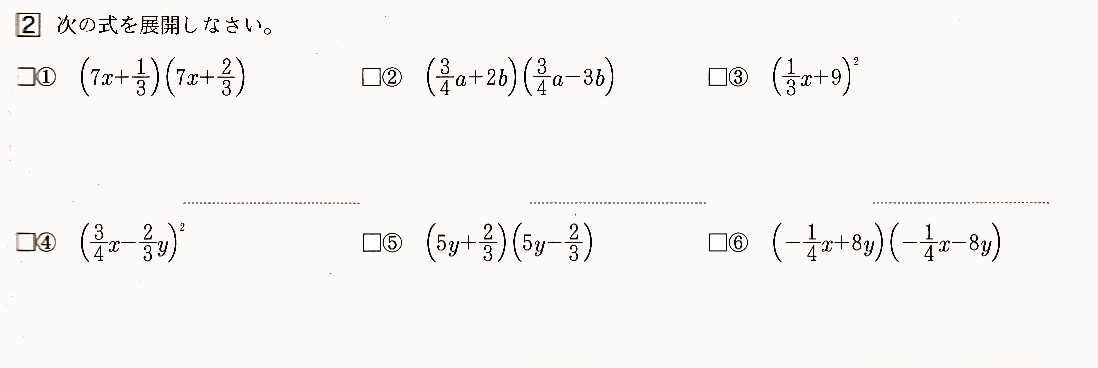
コメント