中学3年数学 式の展開と因数分解 最大公約数と最小公倍数 確認問題2・解答
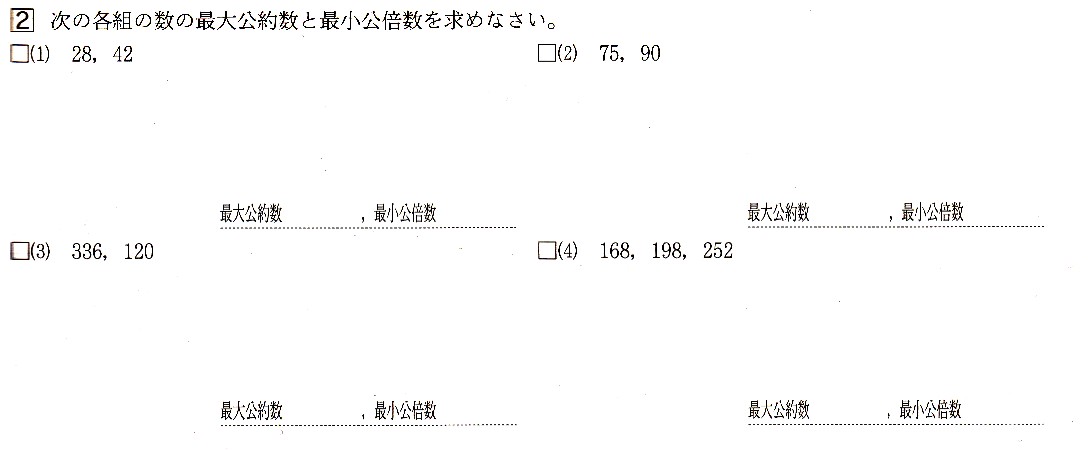
2、次の各組の数の最大公約数と最小公倍数を求めてください。
(1)28、42
まずは素因数分解をします。
2)28 2)42
2)14 3)21
・・・7・・・ 7
最大公約数は共通する素因数をかけたものになりますから、
28=2×2 ×7
42=2 ×3×7
2 × 7=14
最大公約数は14になります。
最小公倍数はすべての素因数をかけたものになりますから、
28=2×2 ×7
42=2 ×3×7
///////2×2×3×7=84
最小公倍数は84になります。
答え 最大公約数 14、最小公倍数 84
(2)75、90
まずは素因数分解をします。
3)75 3)90
5)25 3)30
・・・5 2)10
・・・・・・・ 5
75=3×5² 90=2×3²×5
最大公約数は共通する素因数をかけたものになりますから、
90=2×3×3×5
75= 3× 5×5
3 × 5=15
最大公約数は15になります。
最小公倍数はすべての素因数をかけたものになりますから、
90=2×3×3×5
75= 3× 5×5
///////2×3×3×5×5=450
最小公倍数は450になります。
答え 最大公約数 15、最小公倍数 450
(3)336,120
まずは素因素分解をします。
2)336 2)120
2)168 2) 60
2) 84 2) 30
2) 42 3) 15
3) 21 /////////5
・・・・7
2⁴×3×7=336、2³×3×5=120
最大公約数は共通する素因数をかけたものになりますから、
336=2×2×2×2×3 ×7
120=2×2×2 ×3×5
2×2 × 2 × 3=24
最大公約数は24になります。
最小公倍数はすべての素因数をかけたものになりますから、
336=2×2×2×2×3 ×7
120=2×2×2 ×3×5
/////////2×2×2×2×3×5×7=1680
最小公倍数は1680になります。
答え 最大公約数 24、最小公倍数 1680
(4)168,198,252
因数分解をします。
2)168 2)198 2)252
2) 84 3) 99 2)126
2) 42 3) 33 3) 63
3) 21 ・・・11 3) 21
・・・・7 7
最大公約数は共通する素因数をかけたものになりますから、
168=2×2×2×3 ×7
198=2 ×3×3 × 11
252=2×2 ×3×3×7
/////////2 ×3=6
最大公約数は6になります。
最小公倍数はすべての素因数をかけたものになりますから、
168=2×2×2×3 ×7
198=2 ×3×3 × 11
252=2×2 ×3×3×7
/////////2×2×2×3×3×7×11=5544
最小公倍数は5544になります。
答え 最大公約数 6、最小公倍数 5544










コメント