中学1年数学 直線図形と対称 基本の作図 確認問題4 解答・解説
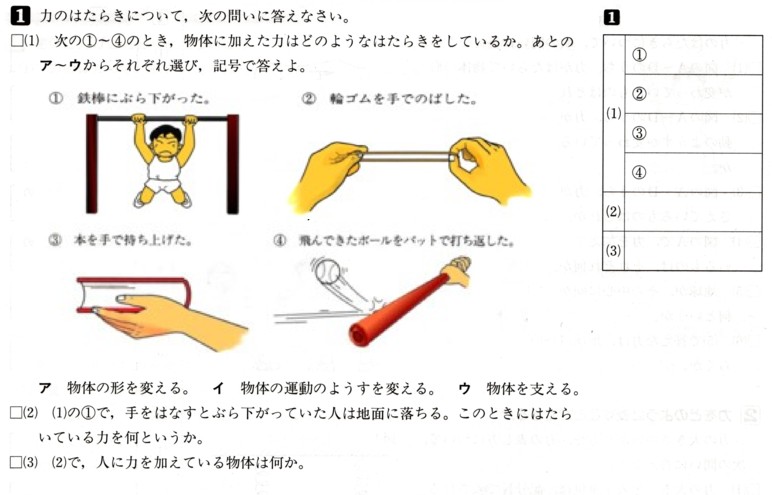
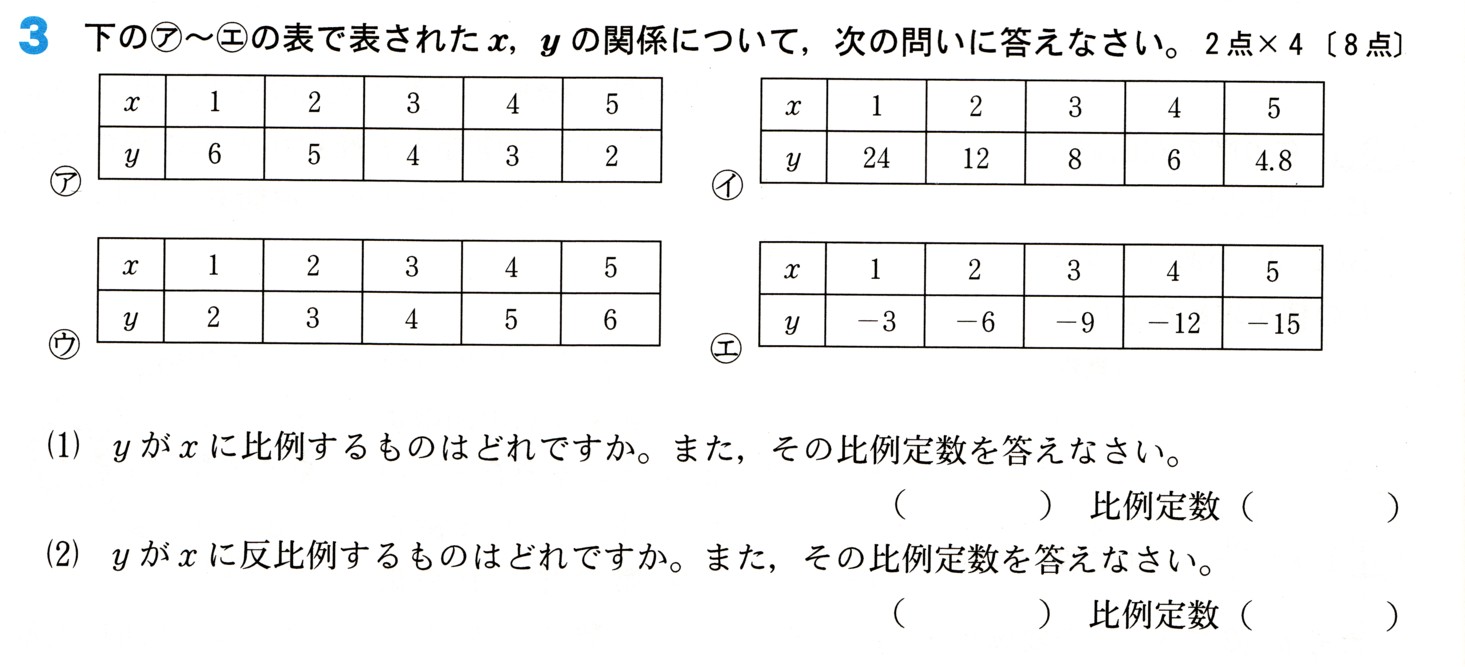
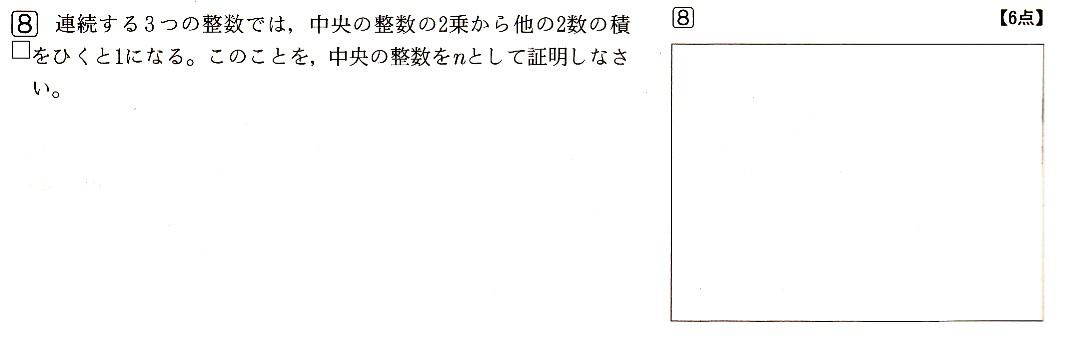
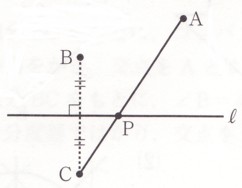
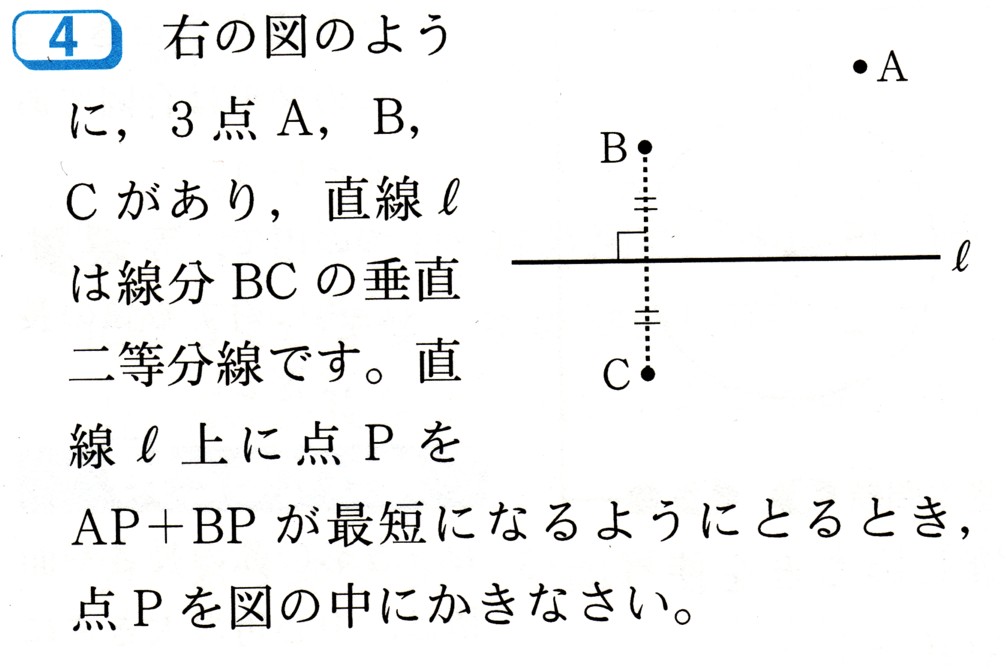
図のように、3点A,B,Cがあり、直線ℓは線分BCの垂直二等分線です。
直線ℓ上に点PをAP+BPが最短になるようにとるとき、点Pを図のなかに
かいてください。
まずは、最短な距離とは何かです? 一番短くなるのは直線ですから、直線
になる方法を考えていきます。
なぜ、この問題には線分BCをはさんで点Cがあるのかです!
線分BCをガラスだと考えてみます、ガラスは明るかったり暗かったりすると、
反射したり透過したりします。点Aの光が線分ℓで反射、すると点Bに、透過する
と点Cと考えると、
点Aと点Cとを直線で結んだ線が最短の長さになり、直線ℓとの交点が点Pにな
ります、この点Pから点Aの距離と点Pから点Cまでの距離は線対称ですから同じ
になります。







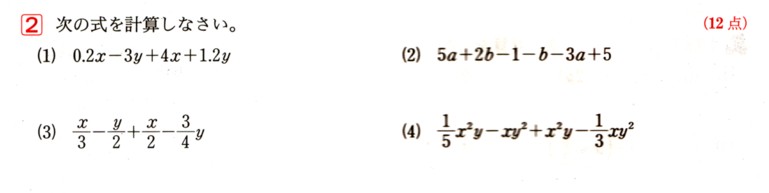







コメント