中学1年数学 円とおうぎ形2 練習問題3 解答・解説
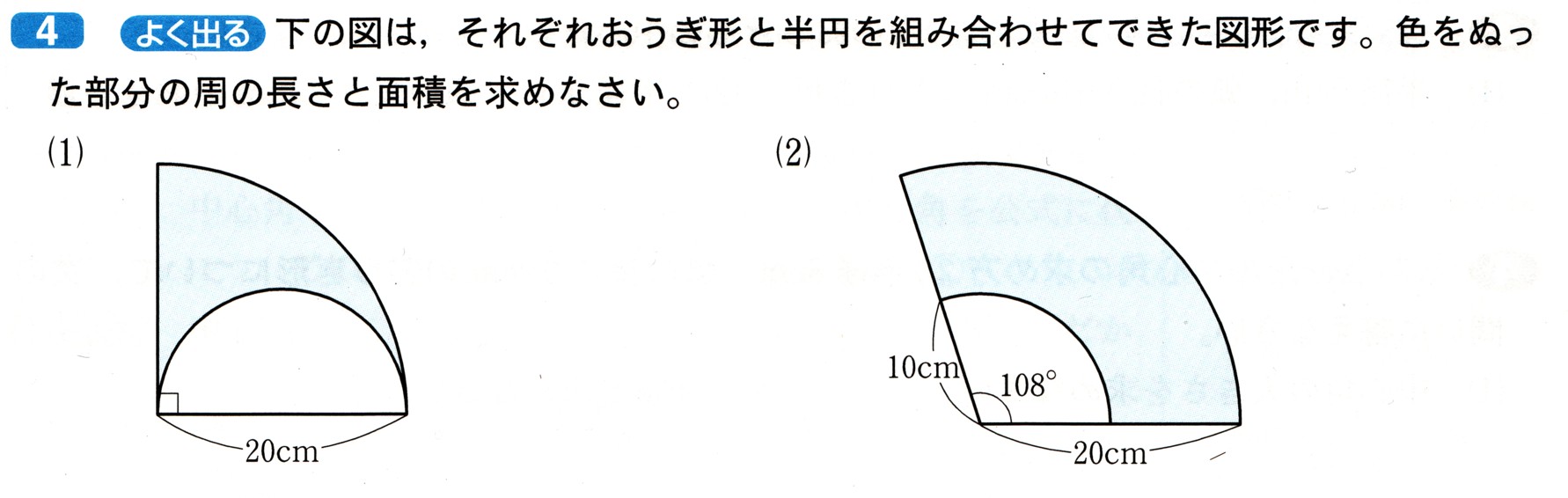
(1)直径が20cmの半円があります。この半円の周の長さと面積を求めてください。
まずは、周の長さから考えます。
半円の周ですから、弧の長さと直径の長さの合計の長さが、この半円の周の
長さになります。
周の長さを求める式は、ℓ=2πγ×a/360
ですから、この式にあてはめていきましょう。
半円ということは、180゜です、
直径が20cmということは半径は10cmになります。
(おうぎ形の弧の長さ)=2π×半径×中心角/360゜
=2π×10×180゜/360゜
=20π×1/2
=10π(cm)
これで、半円の弧の長さがわかりました。
直径は20cmですから
(半円の弧の長さ)+(直径の長さ)=10π+20(cm)
次に、この半円の面積を考えていきましょう。
半円の面積を求める式は、S=πγ²×a/360
でしたね。この式にあてはめていきます。
(おうぎ形の面積)=π×半径×半径×中心角/360゜
=π×10×10×180゜/360゜
=100π×1/2
=50πcm²
答え 周の長さ 10π+20(cm) 、おうぎ形の面積 50πcm²
(2)半径4?、面積12πcm²のおうぎ形の中心角の大きさを求めてください。
今回は、中心角を求めるのですから、
わかっている面積を求める式を利用して考えていきます。
面積を求める式は、S=πγ²×a/360
面積は12πcm²で、半径が4?ですから上の式にあてはめていきます。
(おうぎ形の面積)=π×半径×半径×中心角/360゜
12πcm² =π×4×4×中心角/360゜
12πcm²=16π×中心角/360゜
両辺に360をかけます
12πcm²×360=16π×360×中心角/360゜
次に、1/16πを両辺にかけます
12πcm²×360×1/16π=16π×1/16π×360×中心角/360゜
270=中心角
答え 中心角 270゜
(3)弧の長さが6πcmで、中心角が120゜のおうぎ形の半径を求めてください。
今回は半径を求めるのですが、わかっているのが弧の長さと中心角
ですから、弧の長さの式で考えていきます。
弧の長さを求める式は、
ℓ=2πγ×a/360
弧の長さが6πcm 中心角が120゜
(おうぎ形の弧の長さ)=2π×半径×中心角/360゜
6πcm=2π×半径×120゜/360゜
6πcm=2π×半径×1/3
両辺に3をかけます
3×6πcm=2π×半径3×1/3
両辺に1/2πをかけます
1/2π×3×6πcm=1/2π×2π×半径3×1/3
9(cm)=半径
答え 半径 9?
(4)半径10cmのおうぎ形で、弧の長さが半径4cmの円の周に等しいとき、
このおうぎ形の中心角の大きさを求めてください。
わかっていることを考えていきましょう。
このおうぎ形の半径は10cm
このおうぎ形の弧の長さは、半径4cmの円の周に等しい。
(おうぎ形の弧の長さ)=(半径4cmの円の周)
たずねているのは、弧のおうぎ形の中心角です。
まずは、おうぎ形のこの長さを求めます。
(おうぎ形の弧の長さ)=(半径4cmの円の周)ですから
半径4cmの円周を求めます。
円周の求め方は
ℓ=2πγ
(円周)=2×π×半径
この式に半径4cmをあてはめていきます。
(円周)=2×π×4
=8π
これで、おうぎ形の弧(8π)の長さもわかりました。
次に、おうぎ形の中心角を求めますが、わかっているのは
弧の長さ 8π
半径 10cm
ですから、おうぎ形の弧の長さを求める式から中心角を求めていきましょう。
おうぎ形の弧の長さを求める式は
ℓ=2πγ×中心角/360
ですから、弧の式にわかっているものをあてはめていきましょう。
(おうぎ形の弧の長さ)=2π×半径×中心角/360
8π=2π×10cm×中心角/360
両辺に360をかけます
360×8π=2π×10cm×360×中心角/360
2880π=20π×中心角
次に、両辺に1/20πをかけます
1/20π×2880π=1/20π×20π×中心角
144=中心角
これで、半径10cm、弧の長さ8πのおうぎ形の中心角がわかりました。
答え 144゜











コメント