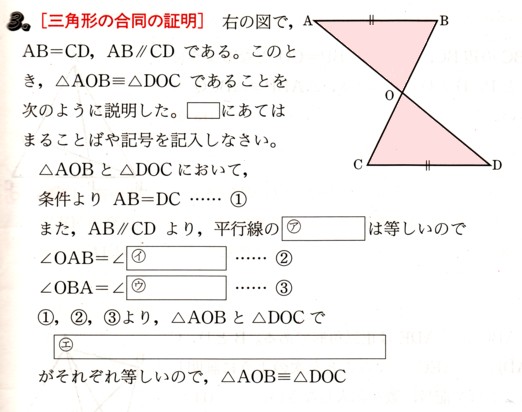
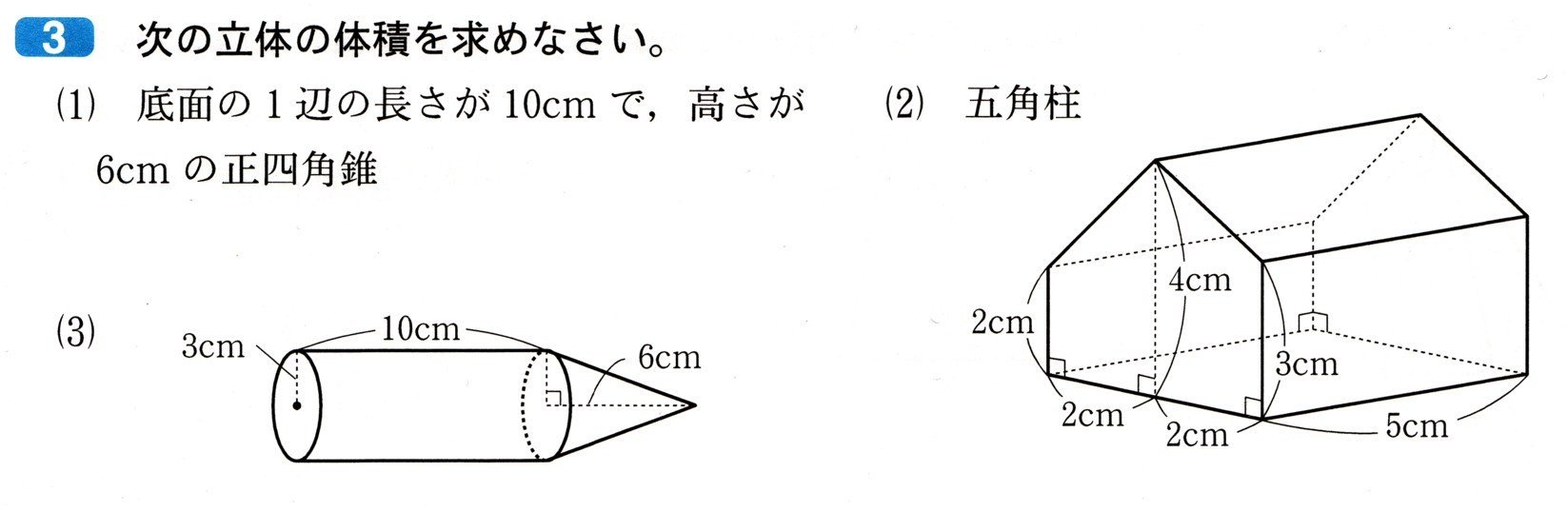
中学1年数学　平面図形　まとめテスト8　解答・解説

中学1年数学　平面図形　まとめテスト8　解答・解説

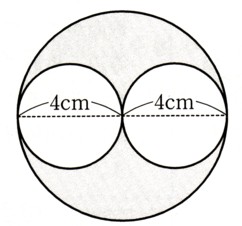
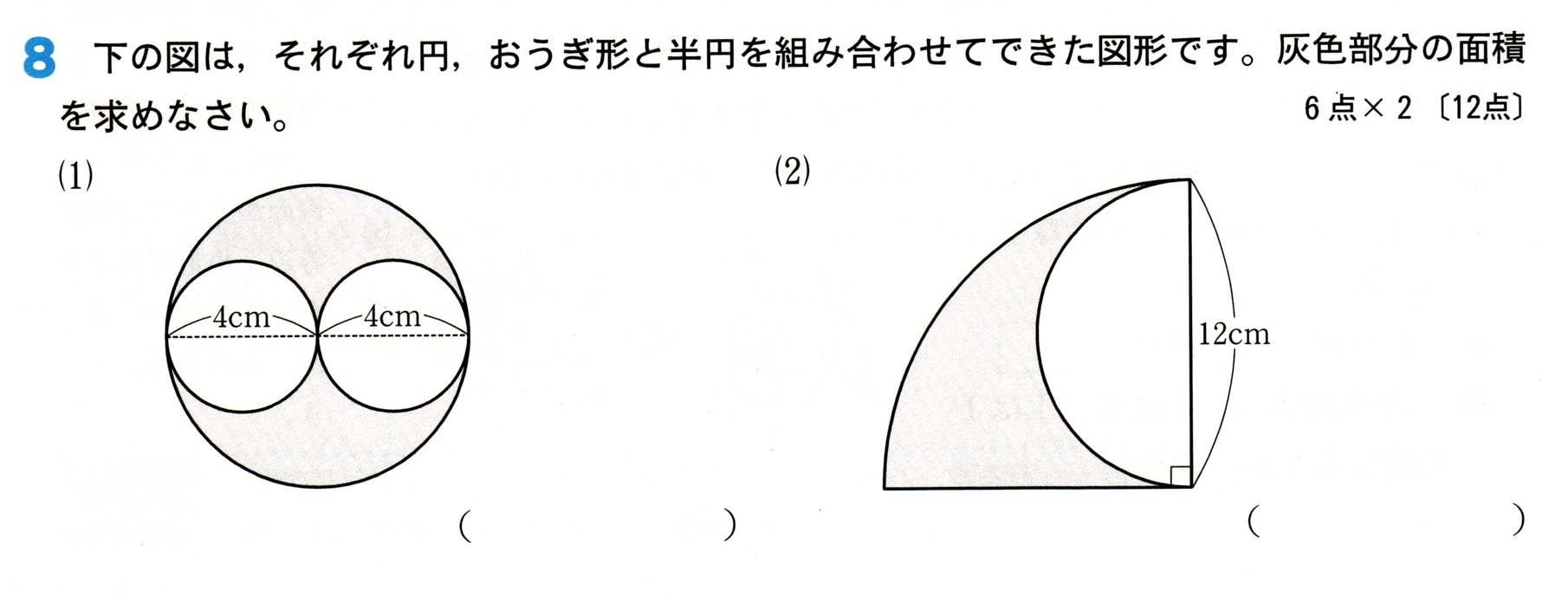
 図はそれぞれ円、おうぎ形と半径を組み合わせてできた図形です。灰色部分の面積を求めてください。

（１）

この図形の面積のだしかたは、全体の円の面積をだして、中の小さい2つの円の面積をひけば

　　　残りの灰色部分の面積がわかります。

　　それでは、大きな円の面積から求めていきましょう

　　半径は、4cm

　　円の面積の求める式は

　　S＝πγ²

　　ですから

　　　(円の面積)＝π×半径×半径

　　　　　　　　＝π×4×4

　　　　　　　　＝16π

　　次に小さな円の面積を求めます

　　同じように円を求める式は

　　S＝πγ²

　　ですから

　　　(円の面積)＝π×半径×半径

　　　　　　　　＝π×2×2

　　　　　　　　＝４π

　　　小さな円は2つありますから

　　　　2×4π＝8π

　　　(大きな円)から(小さな円)をひけば（灰色部分の面積）がわかりますから

　　　　16π　−　　　8π　　　　＝8π

　　面積は?²で表しますから

　　　答え　８π?²
　　

（２）

  この図形は、半径が12cmの円の1/4のおうぎ形ということがわかります。

　　白い部分は、半径が6?の半円ですね、灰色部分は、おうぎ形の面積から、半円の面積を

　　ひけば、灰色部分の面積がわかります。

　　　それでは、まず最初におうぎ形の面積を考えましょう。

　　半径が12cmの円の面積を求め、それを1/4にすれば、この扇形の面積がわかります。

　　正しおうぎ形の面積を求める式を使えば、簡単です！

　　円の面積は

　　S＝πγ²ですから

　　　(円の面積)＝π×半径×半径

　　　　　　　　＝π×12×12

　　　　　　　　＝144π

　　　このおうぎ形は、1/4ですから

　　　　144π×1/4＝36π?²

　　次に半円の面積を求めます

　　　半円の半径は6cm

　　　同じように円の面積を求めてから半分にしましょう。

　　　　(円の面積)＝π×半径×半径

　　　　　　　　　＝π×6×6

　　　　　　　　　＝36π

　　半円ですから半分にします

　　36π×1/2＝18π

　　　おうぎ形の面積から、半円の面積をひけば、灰色部分の面積ですから

　　　　　36π　−　18π　＝　18π?²

　　答え　　18π?²