中学2年数学 式の計算 式の利用 2練習問題4・解答
4、柱体の体積
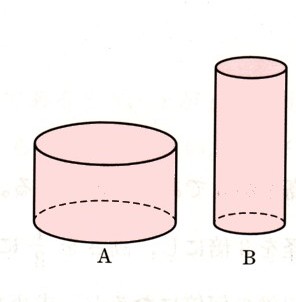
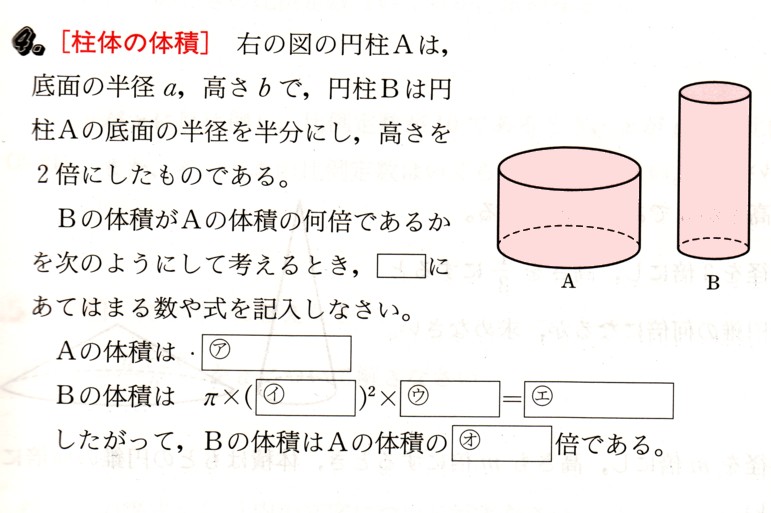
図 の円柱Aは、底面の半径a、高さbで、円柱Bは円柱Aの底面の半径を半分にし、高さを2倍にしたものになります。
の円柱Aは、底面の半径a、高さbで、円柱Bは円柱Aの底面の半径を半分にし、高さを2倍にしたものになります。
Bの体積がAの体積の何倍であるかを次のようにして考えるとき、[ ]にあてはまる数や式を記入してください。
Aの体積は、ア[ ]
Bの体積は π×(イ[ ])²×ウ[ ]=エ[ ]
したがって、Bの体積はAの体積のオ[ ]倍である。
Aの体積は 、底面積×高さ になります。
底面積は円になりますから
半径×半径×π になります。
半径は、aですから。
π×a²×b=πa²b
になります。
Bの体積は
同じ円柱ですが、Aの底面積の半径の半分ですから
Aの半分 (半径×半径×π)÷2 になります。
そして、高さはAの円柱の2倍になりますから
2×b になります。
ですから、
π×(a/2)²×2b=πa²b/2
BはAの何倍かをたずねていますから、
Bの円柱をAの円柱の体積で割れば何倍かがわかります。
したがって、πa²b/2÷πa²b=1/2
になり、1/2倍ということがわかります。
Aの体積は、ア[ πa²b ]
Bの体積は π×(イ[ a/2 ])²×ウ[ 2b ]=エ[ πa²b/2 ]
したがって、Bの体積はAの体積のオ[1/2]倍である。










コメント