1、速さ
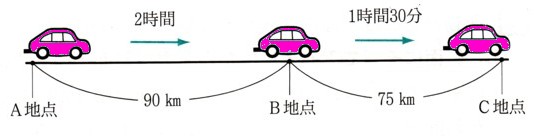
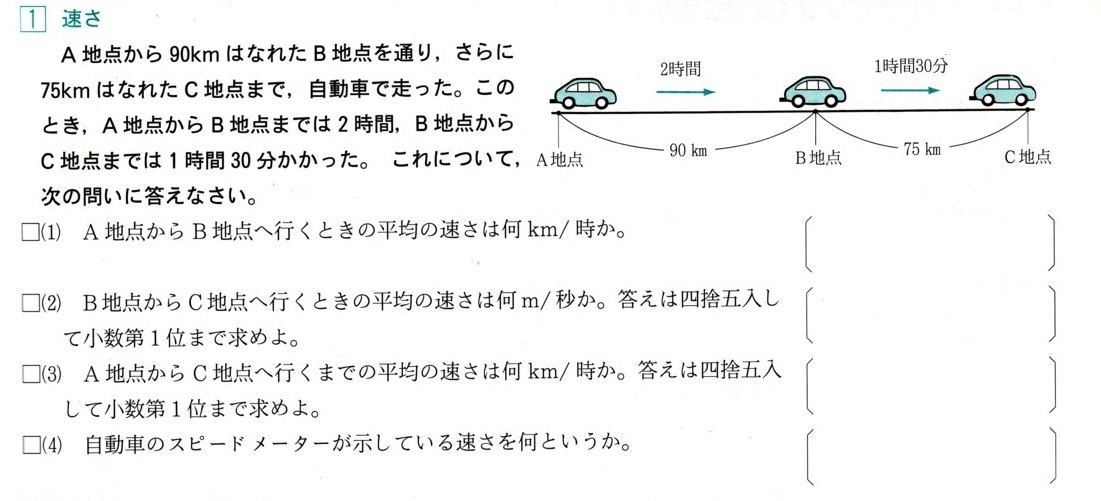
A地点から90km離れたB地点を通り、さらに75km離れたC地点まで、自動車で走りました。
このとき、A地点からB地点までは2時間かかり、B地点からC地点までは1時間30分かかりました。
これについて次の問いに答えてください。
(1)A地点からB地点へ行くときの平均の速さは何km/時かかりましたか?
平均の速さは、移動した距離をかかった時間で割れば求めることが出来ます。
平均の速さ〔m/秒〕=移動距離〔m〕÷ 移動にかかった時間〔秒〕
移動距離〔km〕=90km(A~Bの距離)
移動にかかった時間〔時間〕=2時間(A~Bの移動にかかった時間)
90÷2=45〔km/時〕
答え 45〔km/時〕
(2)B地点からC地点へ行くときの平均の速さは何m/秒になりますか?
答えは四捨五入して小数第1位まで求めてください。
移動距離〔?〕=75km=75×1000m=75000m(A~Bの距離)
移動にかかった時間〔時間〕=1時間30分=60(秒)×90(分)=5400秒(A~Bの移動にかかった時間)
75000(m)÷5400(秒)=13.88888…〔m/秒〕
小数第1位までで四捨五入になりますから、
13.9〔m/秒〕になります。
答え 13.9〔m/秒〕
(3)A地点からC地点へ行くまでの平均の速さは何km/時になりますか?
答えは小数第1位まで求めてください。
移動距離〔km〕
平均の速さ〔km/時〕=
移動にかかった時間〔時間〕
移動距離〔?〕=90+75=165km(A~Cの距離)
移動にかかった時間〔時間〕=2時間+1時間30分=3時間30分=3.5時間(A~Cの移動にかかった時間)
165km÷3.5時間=47.14285…〔?/時〕
小数第1位までで四捨五入になりますから、
47.1〔m/時〕 になります。
答え 47.1〔m/時〕
(4)自動車のスピードメーターが示している速さを何といいますか?

平均をとる時間間隔をどんどん短くしていくと平均の速さは次々と変化していきます。
このような速さを瞬間の速さといいます。
答え 瞬間の速さ







コメント