
今回は、また復習をかねて数学の「文字の式」の練習問題を出題します。
解答
1
(1)① ②
③
④
(2)① ②
2
(1)円 (2)
(分) (3)
(g) (4)
(点)
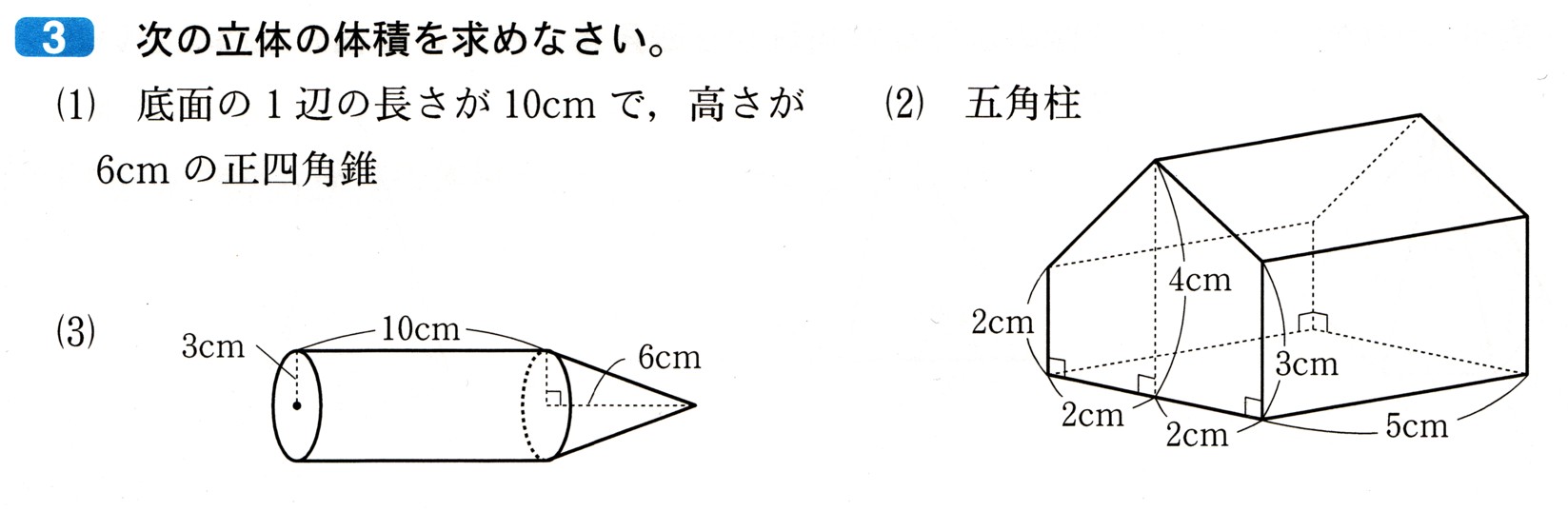
3
(1)-11 (2)12 (3)-3 (4)4
4
(1) (2)
(3)
(4)
5
(1)-3 (2)
6
(1) (2)
(3)
(4)
(5)
(6) (7)
(8)
7
(1) (2)
(3)
(4)
8
(1) (2)
9
解説
2
(2)
(4)得点の合計は、点が二人と
点が一人だから
(点)
7
(1)
(2)
(3)
(4)
9
新たな正三角形を1個つくるのに、マッチ棒は2本必要です、1個目の正三角形には3本のマッチ棒を使っているので、n個つくるのに必要な数は
(本)







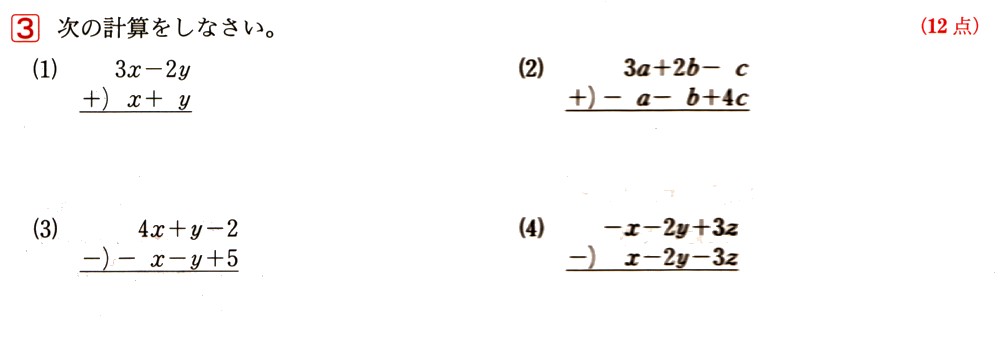




コメント