中学3年数学 平方根 根号を含む式の計算 2確認問題2・解答
2、次の計算をしてください。
①
展開します。
答え
②
展開します。
答え
③
展開します。
答え
④
乗法公式を利用して、展開します。
答え
⑤
乗法公式を利用して展開します。
答え
⑤
答え
⑥
答え
⑦
答え
⑧
答え
 数学
数学  平面図形
平面図形  数学
数学 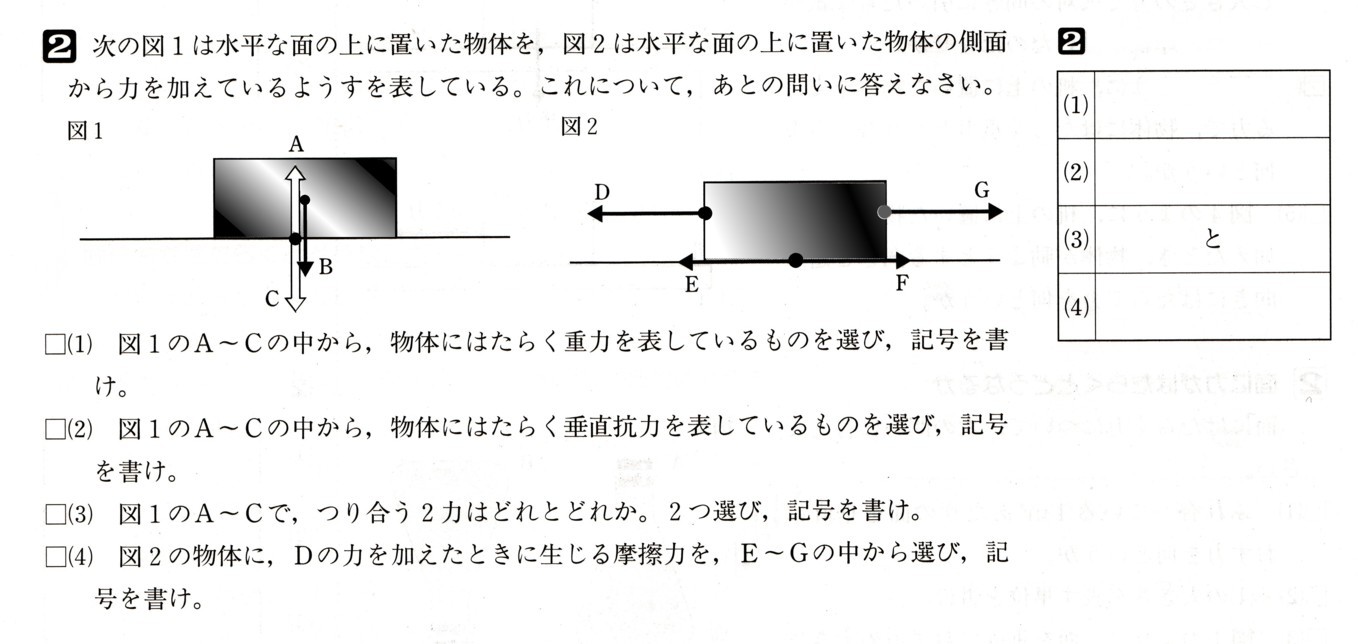 力の世界
力の世界  物質
物質 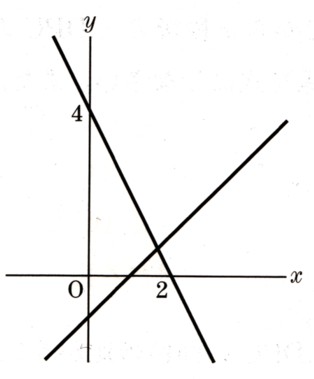 数学
数学 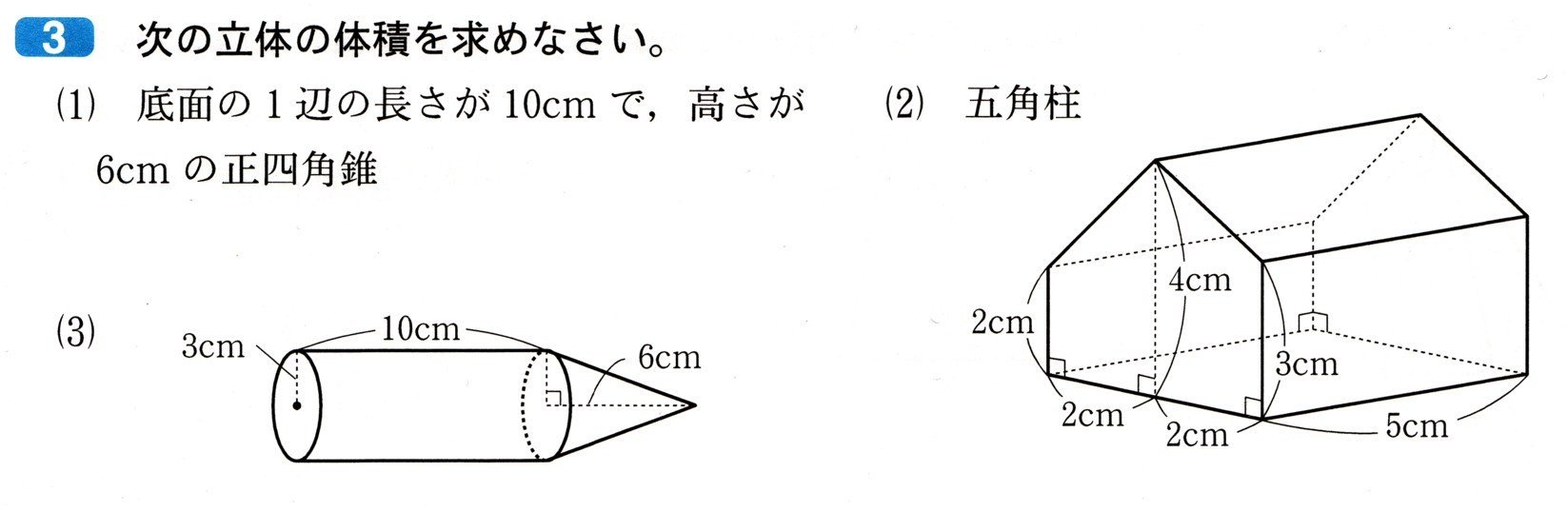 数学
数学 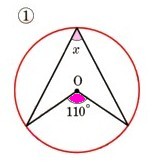 数学
数学  平面図形
平面図形  二次関数
二次関数  数学
数学  平方根
平方根  反比例
反比例  式の計算
式の計算  因数分解
因数分解  数学
数学  物質
物質  一般動詞
一般動詞
コメント