中学２年数学 平面図形 まとめテスト２・解答
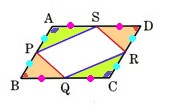
２、平行四辺形ＡＢＣＤの辺ＡＢ、ＢＣ、ＣＤ、ＤＡの中点を、それぞれＰ、Ｑ、Ｒ、Sとするとき、四角形ＰＱＲSは平行四辺形となることを証明してください。
答え 
〔証明〕
△ＡＰSと△ＣＱＲにおいて
仮定より
平行四辺形は向かい合う２つの辺の長さはそれぞれ等しくなりますから
ＡＰ＝ＣＲ・・・①
ＡS＝ＱＣ・・・・②
平行四辺形は向かい合う２つの角はそれぞれ等しくなりますから
∠ＰＡＳ＝∠ＱＣＲ・・・・③
①、②、③より
２つの辺とその間の角がそれぞれ等しくなりますから
△ＡＰS≡△ＣＱＲ
になります。
合同な三角形の対応する辺はそれぞれ等しくなりますから、
辺ＰS＝辺ＱＲ・・・・④
になります。
つぎに、△ＢＰＱと△ＤSＲにおいて 仮定より
平行四辺形は向かい合う２つの辺の長さはそれぞれ等しくなりますから
ＢＰ＝ＤＲ・・・・⑤
ＢＱ＝SＤ・・・・⑥
平行四辺形は向かい合う２つの角はそれぞれ等しくなりますから
∠ＰＢＱ＝∠SＤＲ・・・・⑦
⑤、⑥、⑦より
２つの辺とその間の角がそれぞれ等しくなりますから
△ＢＰＱ≡△ＤSＲ
になります。
合同な三角形の対応する辺はそれぞれ等しくなりますから、
辺ＰＱ＝辺SＲ・・・・⑧
になります。
④、⑧より
向かい合う２つの辺の長さがそれぞれ等しくなりますから
SPＱＲは平行四辺形ということがわかります。
コメント