中学２年数学 図形の調べ方 図形と証明 確認問題4・解答
４、図
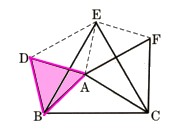
で、△ＤＢＡ，△ＥＢＣ、△ＦＡＣは、それぞれ△ＡＢＣの辺ＡＢ，ＢＣ，ＣＡを1辺とする正三角形である。ＤとＥ，ＥとＦ，ＡとＥを結ぶとき、△ＡＢＣと合同な三角形をすべていって下さい。
で、△ＤＢＡ，△ＥＢＣ、△ＦＡＣは、それぞれ△ＡＢＣの辺ＡＢ，ＢＣ，ＣＡを1辺とする正三角形である。ＤとＥ，ＥとＦ，ＡとＥを結ぶとき、△ＡＢＣと合同な三角形をすべていって下さい。 ［証明］
△ＡＢＣと△ＢＤＥについて
△ＢＣＥは正三角形ですから
ＢＣ＝ＢＥ・・・①
△ＡＢＤは正三角形ですから
ＡＢ＝ＢＤ・・・②
△ＢＤＡ、△ＢＣＥ、△ＡＣＦも正三角形ですから、
∠ＤＢＡ＝60°
∠ＥＢＣ＝60°
∠ＤＢＥ＝∠ＤＢＡー∠ＥＢＡ
∠ＡＢＣ＝∠ＥＢＣー∠ＥＢＡ
∠ＤＢＥ＝60°ー∠ＥＢＡ
∠ＡＢＣ＝60°ー∠ＥＢＡ
∠ＤＢＥ＝∠ＡＢＣ・・・③
①、②、③より
△ＡＢＣ≡△ＢＤＥ
つぎに、△ＡＢＣと△ＣＥＦについて
仮定により、
△ＢＣＥは正三角形ですから
ＢＣ＝ＣＥ・・・①
△ＡＣＦは正三角形ですから
ＡＣ＝ＣＦ・・・②
仮定により、
△ＢＤＡ、△ＡＣＦ、△ＢＣＥも正三角形ですから、
∠ＦＣＡ＝60°
∠ＥＣＢ＝60°
∠ＦＣＥ＝∠ＦＣＡー∠ＥＣＡ
∠ＡＣＢ＝∠ＥＣＢー∠ＥＣＡ
∠ＦＣＥ＝60°ー∠ＥＣＡ
∠ＡＣＢ＝60°ー∠ＥＣＡ
∠ＦＣＥ＝∠ＡＣＢ・・・③
①、②、③より
△ＡＢＣ≡△ＣＥＦ
になります。
答え △ＢＤＥ、△ＣＥＦ
コメント