中学2年数学　1次関数　1次関数の応用　確認問題１・解答

中学2年数学　1次関数　1次関数の応用　確認問題１・解答

１、次の図で、四角形ＡＢＣＤは、ＡＢ＝20cm、ＢＣ＝10cm、の長方形で、点Mは、辺ＣＤの中点になります。

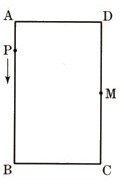
　点ＰはＡを出発して矢印の方向に、この長方形の辺上をＣまで動くものとします。点Ｐの動く早さを毎秒1?として、次の問いに答えて下さい。

（１）点Ｐが辺ＡＢ上にあって、四角形ＡＰＣＭの面積が７０㎠になるのは、点ＰがＡを出発して何秒後になりますか？求めて下さい。

 　　まずは、点Ｐが中点に来たとしたら、10cmですから、四角形ＡＰＭＤは正方形になりますから、

　　面積は10×10＝100㎠になります、

　　四角形ＡＰＣＭの面積は、７０㎠ですから、台形になると考えられます。

　　　台形の面積を求める式は

　　(上底＋下底)×(高さ)×1/2＝(台形の面積)㎠

　　になります。

　　(台形の面積)＝70㎠

　　(上底)＝辺ＤＭ＝10cm

　　(下底)＝辺ＡＰ＝〔秒速1?〕×[時間]

　　(高さ)＝辺ＡＤ＝10cm

　　　時間(秒)をχとします。

　　(10＋χ)×10÷2＝70

　　
　　(10＋χ)×10
　　――――――　＝70
　　　　　2

　　　になります。

　　χが時間ですからχがわかれば、点Pが70㎠の位置に来る時間がわかります。

　　(10＋χ)×10＝140

　　100＋10χ＝140

　　10χ＝140−100

　　10χ＝40

　　χ＝4

　　　答え　4秒後 

（２）点PがAを出発してからχ秒後の△ＡＰＭの面積をｙ㎠とするとき、20≦χ≦30　におけるｙをχの式で表して下さい。

　　χの変域が20～30ということは、20(秒)～30(秒)　ということになります。

　　進む距離で考えると、秒速1?ですから、20～30(?)進むと考えられます。

　　点Ｐが20～30(?)進むと、辺ＡＢ＝20?、辺ＢＣ＝10cm　ですから。

　　点Ｐは、辺ＢＣ上にあると考えられます。

　　図をみてみます。

　　□ＡＢＣＤ−（△ＡＭＤ＋△ＡＢＰ＋△ＣＭＰ）＝△ＡＭＰの面積

　　□ＡＢＣＤは、20×10＝200㎠

　　△ＡＭＤは、変わりませんから　10×10÷2＝50㎠

　　△ＡＢＰは、時間がたてば面積は増えますし

    △ＣＭＰは、時間がたてば面積が減ります。

　　三角形の面積は、(底辺)×(高さ)÷2

　　△ＡＢＰの高さは、20cm

　　△ＣＭＰの高さは、10cm

　　問題は、底辺になります。

　　仮に25秒とします。

　　点Pは変BC上の中間にあります。

　　底辺の長さ(距離)は、面積が増加する場合は　25(秒)−20(秒)　の位置にあります。

　　　　　　　　　　　　面積が減少する場合は　30(秒)−25(秒)　の位置にあります。　　

　　25(秒)が、掛かった時間ですから、χに置き換えると、

　　　面積が増加する場合　χ−20

　　　面積が減少する場合　30−χ

　　これで、2つの△の底辺の長さがわかりました。

　　△ＡＢＰの面積＝20×(χ−20)÷2

　　△ＣＭＰの面積＝10×(30−χ)÷2

　　最初の式にあてはめてみます。

　　　□ＡＢＣＤ−（△ＡＭＤ＋△ＡＢＰ＋△ＣＭＰ）＝△ＡＭＰの面積

　　　　200㎠　−｛50㎠＋20×(χ−20)÷2＋10×(30−χ)÷2｝

　　＝200−（50＋10χ−200＋150−5χ）

　　＝200−(10χ−5χ−200＋150＋50)

　　＝200−5χ

　　△ＡＭＰの面積の式がわかりました。

　　　答え　−5χ＋200