中学2年数学　1次関数　2まとめテスト1・解答

中学2年数学　1次関数　2まとめテスト1・解答

１、次の問いに答えて下さい。

（１）直線　　ｙ＝ａχ−1　が、2点Ａ（１，３），Ｂ（４，２）を結ぶ線分ＡＢと交点を持つとき、ａのとりえる値の範囲を求めて下さい。

　　ｙ＝ａχ−1　は、(傾き)＝ａ、(切片)＝−1　になります。

  ｙ＝ａχ−1　　に（χ、ｙ）＝（１，３）、（χ、ｙ）＝（４，２）を代入します。

　　ａ−1＝3　　　　　　2＝4ａ−1

　　ａ＝3＋1　　　　　　4ａ−1＝2

　　ａ＝4　　　　　　　　4ａ＝2＋1

　　　　　　　　　　　　　ａ＝3/4　

　　　答え　3/4≦ａ≦4  

（２）直線　ｙ＝χ＋ｂ　が、3点Ｏ（０，０），Ａ（１，３），Ｂ（４、−１）を頂点とする△ＯＡＢと交わるとき、ｂのとりえる値の範囲を求めて下さい。

　　　　ｙ＝χ+ｂは、（傾き）1　、(切片)　ｂの直線になります。

　　　　3＝1＋ｂ　　　　　　　　−1＝4＋ｂ

　　　　ｂ＝3−1　　　　　　　　ｂ＝−4−1

　　　　ｂ＝2　　　　　　　　　　ｂ＝−5

　　　　
　　　　答え　−5≦ｂ≦2  

（３）3直線　ｙ＝χ＋1、ｙ＝−2χ＋7、ｙ＝ａχ＋4　が三角形を作らないとき、ａの値を求めて下さい。

　　　3直線で、三角形ができないのは、2本の直線が平行か、3直線が1点で交わる場合になります。

      ｙ＝χ＋1　と　ｙ＝−2χ＋7　は、（傾き）と（切片）がわかっていますから、直線が、かけます。

　　2本の直線が、平行ということは、

　　ｙ＝χ＋1　と　ｙ＝ａχ＋4　が、平行ということは、（傾き）は同じになります。ａ＝1

　　ｙ＝−2χ＋7　と　ｙ＝ａχ＋4　が、平行ということは、（傾き）は同じになります。ａ＝−2

　　3直線が交わる場合は、

　　ｙ＝χ＋1　と　ｙ＝−2χ＋7　の交点になります。

　　
　　ａを出すためには、2直線の交点を出し、その2直線の座標（χ、ｙ）を　ｙ＝ａχ＋4　に代入して求めることができます。

　　2直線の交点を出すために、連立方程式をつくります。

　　　ｙ＝χ＋1
　｛
　　　ｙ＝−2χ＋7

　　χ＋1＝−2χ＋7

　　χ＋2χ＝7−1

　　　3χ＝6

　　　χ＝2

　　ｙ＝2＋1

　　ｙ＝3

　　2直線の座標（χ、ｙ）＝（２，３）がわかりました。

　　　2直線の座標（χ、ｙ）＝（２，３）を　ｙ＝ａχ＋4　に代入します。

　　　3＝2ａ＋4

　　　2ａ＋4＝3

　　　2ａ＝3−4

　　　2ａ＝−1

　　　ａ＝−1/2

　　　答え　ａ＝−1/2　、ａ＝1　、ａ＝−2 

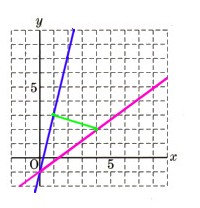
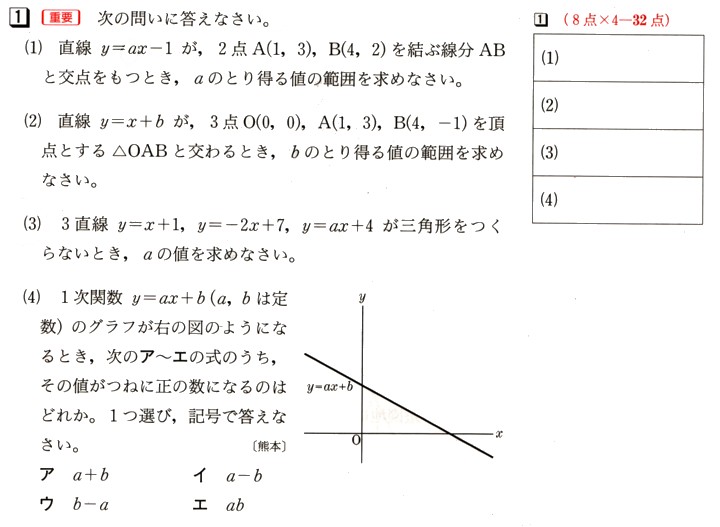
（４）1次関数　ｙ＝ａχ＋ｂ(ａ、ｂは定数)のグラフが図のようになるとき、次のア～エの式のうち、その値が常に正の数になるのはどれになりますか？1つ選んで下さい。

　ア、ａ＋ｂ
　イ、ａ−ｂ
　ウ、ｂ−ａ
　エ、ａｂ

　　ｙ＝ａχ＋ｂ　は、

　　ｙ＝（傾き）χ＋（切片）

　　グラフを見ると、右下がりですから、符号は（−）になります。

　　ａ＜0　ということになります。

　　（切片）は、ｙ軸に接する座標（0、ｂ＞0）になります。

　　0以上ですから符合は（＋）になります。

　　−ａ、＋ｂ　ですから、

　　　答え　ウ