中学2年数学 連立方程式 連立方程式の応用 確認問題1・解答
1、費用・人数の問題
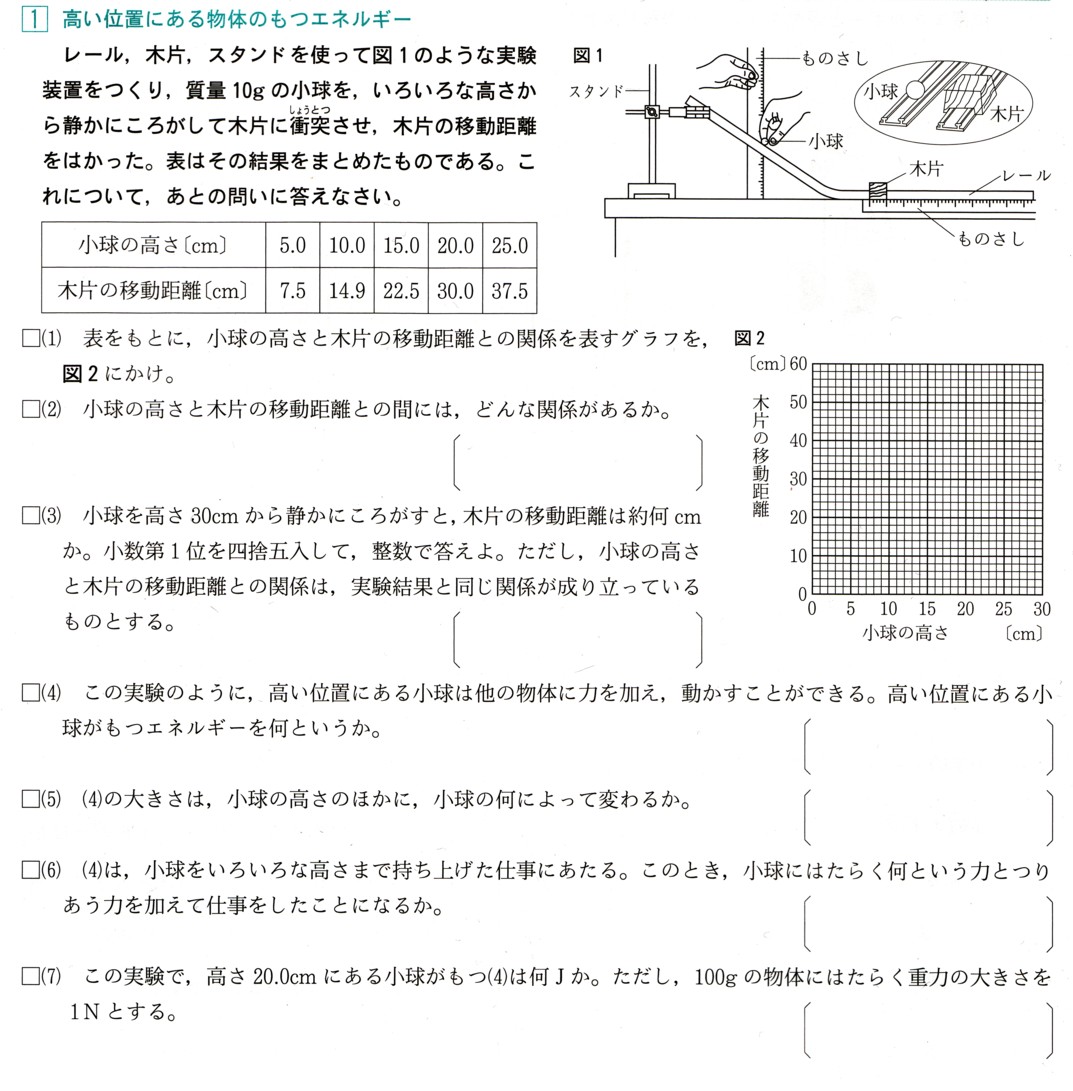
「グループの実習材料費を集金するのに、1人700円ずつ集めると800円不足し、900円集めると400円余ります。材料費と人数を求めてください。」
この問題について。[ ]に適する数、または式を答えてください。
不足している、余る を考えてみます。
700円ずつ集めるということは、(人数)×(700円)=集めた材料費+800
* =で結ばれていますから、800円不足した状態では等号になりません、そのため不足している金額を加えることによって等号にします。
900円ずつ集めるということは、(人数)×(900円)=集めた金額−400
* =で結ばれていますから、400円余るということは、右辺のほうが400円分多くなり等号にはなりません。等号にするために400円分右辺から引き等号にします。
実習材料費をχ(円)、グループの人数をy(人)とすると、
700円ずつで、800円不足するから、χ=[ア 700y+800 ]・・・?
900円ずつで、400円余りますから、χ=[イ 900y−400 ]・・・?
?,?を連立方程式として解くと、
700y+800=χ
{
900y−400=χ
700y+800=900y−400 ということになりますから、
700y−900y=−400−800
−200y=−1200
y=6
700y+800=χ に y=6 を代入します。
700(6)+800=χ
4200+800=χ
5000=χ
材料費[ウ 5000 ]円、人数[エ 6 ]人となります。
答え ア、700y+800 イ、900y−400 ウ、5000 エ、6







コメント