中学2年数学　式の計算　式の乗法・除法　基本問題・解答

中学2年数学　式の計算　式の乗法・除法　基本問題・解答

１、式の乗法

　　　単項式の乗法（除法）では、各文字ごとに積を考えます。

　　?乗法の決まり

　　　　A‵×A゛＝A‵+゛

　　　係数どうしの積と、文字どうしの積を求めて、それらを掛け合わせます。

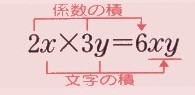
　　　　例：　2χ×3y＝6χy

　　?単項式の乗法では、係数どうしの ｱ〔和・積〕と、文字どうしの ｲ〔和・積〕を求め、それらを掛け合わせます。

　　　−2χ×5y＝(ｳ[　]×5 )×(χ×y)＝ｴ[　　]

２、累乗

　　　5×5や、χ×χ×χは、それぞれ5²、χ⁵と表します。このように、同じ数や文字をいくつか掛け合わせたものを累乗といいます。

　　　○　a²

　　　　　　　右肩に小さくかかっている数を指数といいます。

　　　同じ文字どうしの積は、累乗の指数を使って表します。

　　　　例：　a×a＝a²

　　　　　　　2a²×3a³＝6a⁵

　　?同じ文字の積は、累乗の〔ｱ 指数・係数〕を使って累乗の形にまとめることができます。

　　　χ×χ³＝ｲ[　　　]

３、式の除法 

(1)、除法の決まり

　　　　‵＞゜のとき　A‵÷A゜＝A‵⁻゜

　　　　‵＜゜のとき　A‵÷A゜＝A1／A ゜ｰ‵

　　割る式の逆数を掛ける乗法に直して計算します。

　　　　例：　6ab÷2a＝6ab×1/2a

(2)、多項式÷数

　　　　(多項式)÷(数)では、割る数の逆数をかけ、分配法則にしたがって計算をします。

　　　　(a＋b)÷m＝(a＋b)×1/m＝a/m＋b/m

 　  ?単項式の除法では、割る式の ｱ[　　　]を掛ける乗法に直してから計算します。

　　　6a²÷3a＝6a²×ｲ[　]

　　　　　　　＝6a²／3a

　　　　　　　＝ｳ[　　　]

＊POINT

　　(-a)²と−a²の違いに注意してください。

　(−a)²を計算すると、(−a)×(−a)＝a²　になり、−a²にはなりません。このような場合は混同して間違いやすいのでミスにつながりやすいです。

【解答】

?単項式の乗法では、係数どうしの ｱ〔×和・○積〕と、文字どうしの ｲ〔×和・○積〕を求め、それらを掛け合わせます。

　　　−2χ×5y＝(ｳ[−2]×5 )×(χ×y)＝ｴ[−10χy]

?同じ文字の積は、累乗の〔ｱ ○指数・×係数〕を使って累乗の形にまとめることができます。

　　　χ×χ³＝ｲ[χ⁴]

?単項式の除法では、割る式の ｱ[逆数]を掛ける乗法に直してから計算します。

　　　6a²÷3a＝6a²×ｲ[1/3a]

　　　　　　　＝6a²／3a

　　　　　　　＝ｳ[2a]