中学2年数学　1次関数　1次関数のグラフと式の求め方　確認問題4・解答

中学2年数学　1次関数　1次関数のグラフと式の求め方　確認問題4・解答

４、次の1次関数のグラフを書いて下さい。

　?　ｙ＝3χ−2

　?　ｙ＝−χ＋2

　?　ｙ＝3/2 χ − 1

　?　ｙ＝−1/3 χ ＋ 3

　?　ｙ＝3χ−2

　　　ｙ＝ａχ＋ｂ

　　　ｙ＝(傾き)χ＋(切片)
　　　　　　　　　　　　　　　　　　　　(ｙの増加量)　　　　 3
　(傾き)＝3＝(変化の割合)＝―――――――　＝――
　　　　　　　　　　　　　　　　　　　(χの増加量)　　　　　1

　　　(ｙの増加量)＝3

　　　(χの増加量)＝1

　　　(傾き)が正の符号（＋）ですから、右上がりの直線になります。

　　　(切片)＝−2

　　　　ですから、ｙ軸上の−2を通ります。　　　

　　答え　 

　?　ｙ＝−χ＋2

　　　ｙ＝ａχ＋ｂ

　　　ｙ＝(傾き)χ＋(切片)
　　　　　　　　　　　　　　　　    　(ｙの増加量)　　　　　1
(傾き)＝−1＝(変化の割合)＝―――――　＝−――
　　　　　　　　　　　　　　　　   　(χの増加量)　　　　　1

　　　(ｙの増加量)＝1

　　　(χの増加量)＝1

　　　(傾き)が負の符号（−）ですから、右下がりの直線になります。

　　　(切片)＝＋2

　　　　ですから、ｙ軸上の＋2を通ります。　　　

　　答え　　　

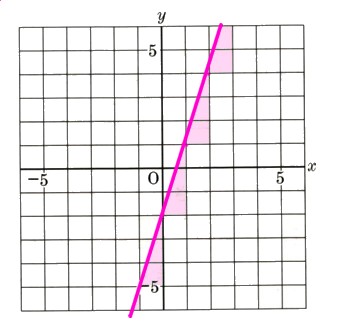
　?　ｙ＝3/2 χ − 1

　　ｙ＝ａχ＋ｂ

　　　ｙ＝(傾き)χ＋(切片)

　　　　　　3　　　　　　　　　　　　　(ｙの増加量)　　3
(傾き)＝――＝(変化の割合)＝―――――＝――
　　　　　　2　　　　　　　　　　　　(χの増加量)　　　2

　　　(ｙの増加量)＝3

　　　(χの増加量)＝2

　　　(傾き)が正の符号（＋）ですから、右上がりの直線になります。

　　　(切片)＝−1

　　　　ですから、ｙ軸上の−1を通ります。　　　

　　答え　 

　?　ｙ＝−1/3 χ ＋ 3

　　ｙ＝ａχ＋ｂ

　　　ｙ＝(傾き)χ＋(切片)

　　　　　　　1　　　　　　　　　　　　　(ｙの増加量)　　　　　1
(傾き)＝−―＝(変化の割合)＝−―――――　＝−―
　　　　　　　3　　　　　　　　　　　　(χの増加量)　　　　　3

　　　(ｙの増加量)＝1

　　　(χの増加量)＝3

　　　(傾き)が負の符号（−）
ですから、右下がりの直線になります。

　　　(切片)＝＋3

　　　　ですから、ｙ軸上の＋3を通ります。　　　

　　答え