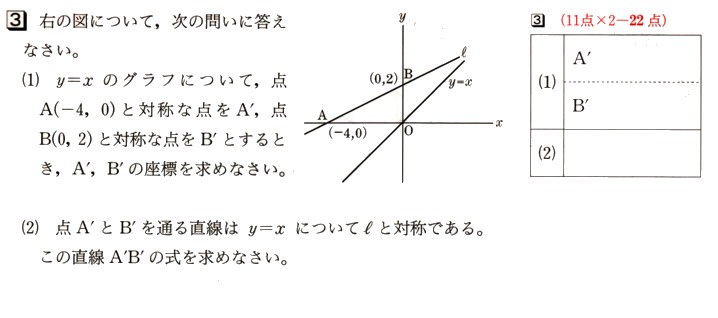
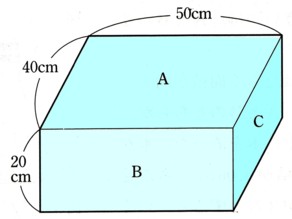
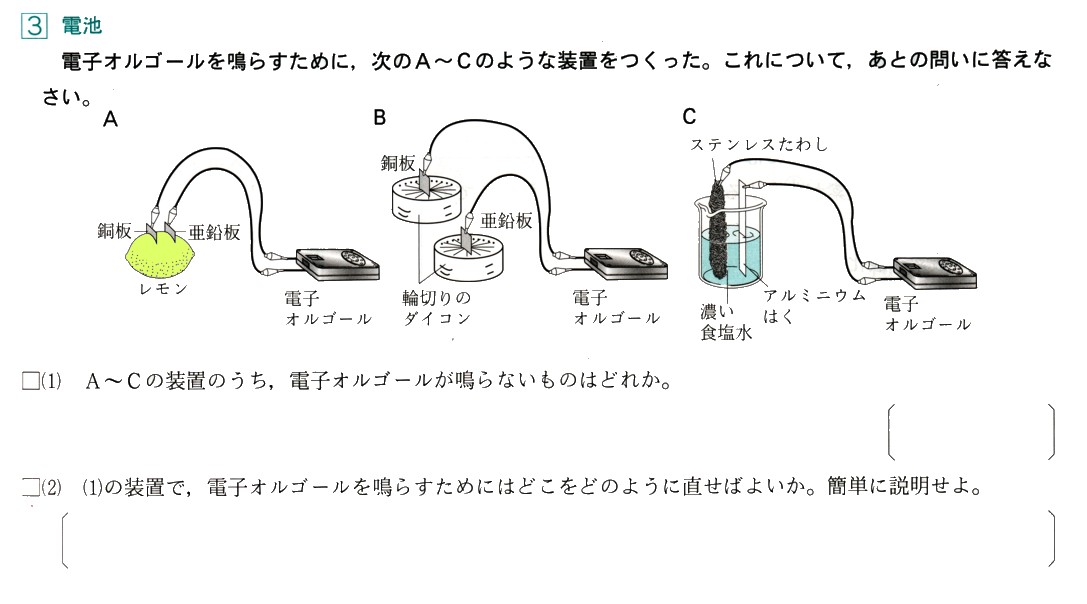
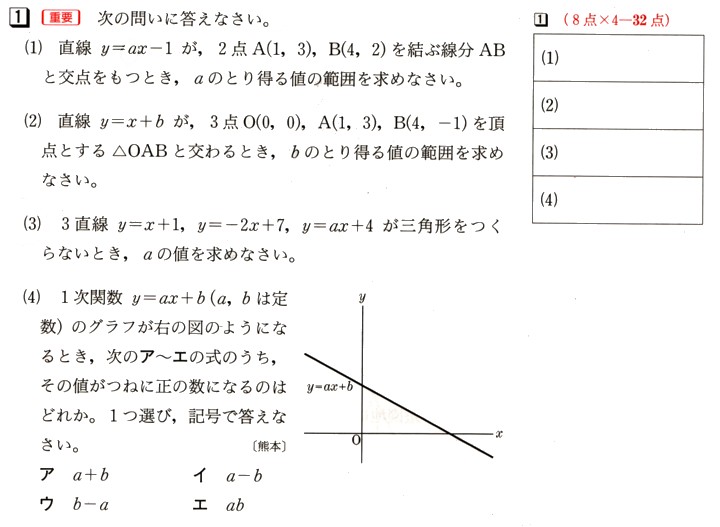
中学2年数学 1次関数 1まとめテスト1・解答
1、次の問いに答えて下さい。
(1)1次関数 y=2χ+a について、χの変域が 1≦χ≦3 のとき、yの変域が −1≦y≦b になります。このとき、a、bの値を求めて下さい。
y=2χ+a に、χの変域、(最小値) 1 、のときyの変域、(最小値) −1 を代入します。
−1=2×1+a
2+a=−1
a=−1−2
a=−3
y=2χ+a に、a=−3 を代入し、χの変域の(最大値)3 を代入します。
y=2×3−3
y=6−3
y=3
答え a=−3、b=3
(2)1次関数 y=aχ+3 について、χの変域が 0≦χ≦6 のとき、yの変域は 1≦y≦3 であります。このとき、aの値を求めて下さい。
y=aχ+3 にχの変域の(最大値) 6 を代入します。yの変域の(最大値) 3 を代入しても式が成立しません。
3=6a+3
6a=0
a=0
y=aχ+3 にχの変域の(最大値) 6 を代入します。yの変域の(最小値) 1 を代入します。
1=6a+3
6a+3=1
6a=1−3
6a=−2
a=−2/6
a=−1/3
答え a=−1/3
(3)y−2が χ−3に比例し、比例定数が−2であるとき、χ=9に対応するyの値はいくつになりますか?
比例ですから、下のような式が成り立ちます。
(y−2)=(比例定数)(χ−3)
(y−2)=(−2)(χ−3)
(y−2)=(−2)(χ−3)に χ=9 を代入します。
(y−2)=(−2)(9−3)
(y−2)=−18+6
y=−18+6+2
y=−10
答え y=−10













コメント