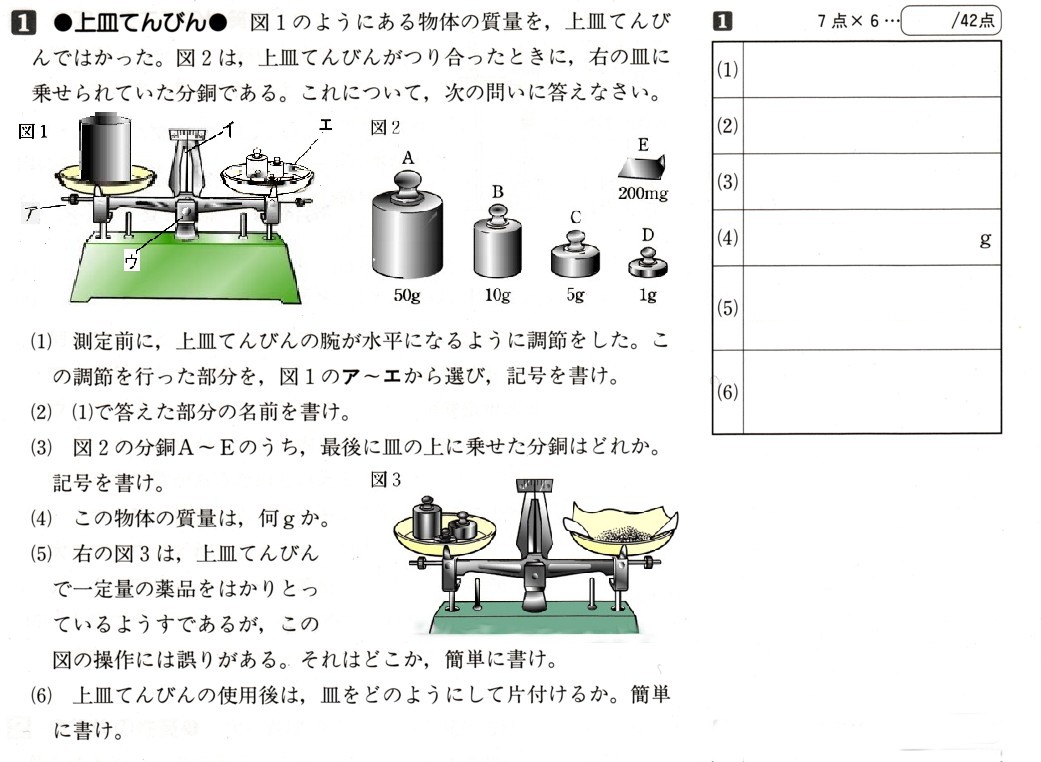
中学2年数学 1次関数 2まとめテスト2・解答
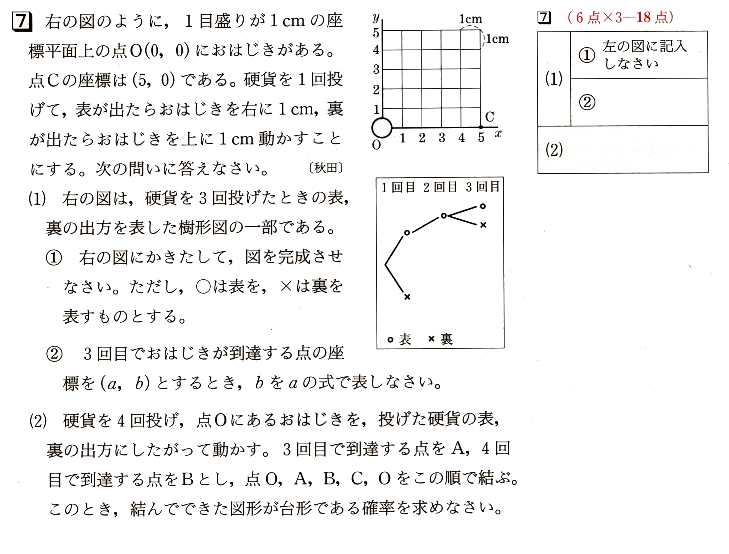
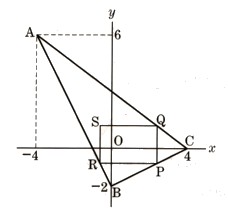
2、図 のように、3点A(−4,6),B(0、−2),C(4,0)を頂点とする△ABCがあります。辺BC上の点Pに対して、辺AC上に点QをPQとy軸が平行になるように取り、辺AB上に点RをPRとχ軸が平行になるように取ります。
のように、3点A(−4,6),B(0、−2),C(4,0)を頂点とする△ABCがあります。辺BC上の点Pに対して、辺AC上に点QをPQとy軸が平行になるように取り、辺AB上に点RをPRとχ軸が平行になるように取ります。
さらに、四角形PQSRが長方形になるように点Sを取るとき、次の問いに答えて下さい。
(1)点Pのχ座標をaとするとき、PQの長さをaの式で表して下さい。
PQの長さを求めるには、
? 直線AC上のQ点と直線BC上のP点の座標を求めます。
ただし、2つの座標のχはaですから、yを求めます。
? Q点とP点の2つの座標がわかれば、点Qから点Pの2つのy座標を引けば直線PQの長さがわかります。
y=aχ+b の形にします。
点Aの座標(−4,6)、点Cの座標(4,0)を2元1次式で考えます。
6=-4a+b
{
0=4a+b
-4a+b=6
{
4a+b=0
-4a+b=6
−) 4a+b=0
−8a=6
a=−3/4
0=4a+b に a=−3/4 を代入します。
−4(−3/4)=b
b=3
y=−3/4χ+3 直線ACの式になります。ただし、χの値がaになりますから、
y=−3/4a+3 となります。
点Bの座標(0,−2)、点Cの座標(4,0)を2元1次式で考えます。
−2=0+b
{
0=4a+b
−2=b
{
−4a=b
−4a=−2
a=2/4
a=1/2
y=1/2χ−2 直線BCの式になります。ただし、χの値がaになりますから、
y=1/2a−2 となります。
座標P(χ、y)=(a、1/2a−2)、座標Q(χ、y)=(a、−3/4a+3) になります。
2つの座標がわかりましたから、
(点Qのy座標)−(点Pのy座標)=(直線PQの長さ)
(−3/4a+3)−(1/2a−2)=−3/4a+3−1/2a+2
=−3/4a−2/4a+3+2
=−5/4a+5
これで、直線PQの長さがわかりました。
答え −5/4a+5
(2)四角形PQSRが正方形になるとき、点Pのχ座標を求めて下さい。
正方形になるには、辺PQと辺PRの長さが等しければ正方形になります。
辺PQの長さはわかっていますから、辺PRが判ればいいということになります。
点Pの座標(a、−3/4a+3)は、わかっていますから点Rの座標を考えます。
点Rの座標の、y軸は点Pのy座標と同じになりますから、−3/4a+3 となります。
χの座標をだすために、直線ABの式に、点Rのχ座標を入れyの座標を求めます。
直線ABの式は、
(yの増加量) 6+2 2
(傾き)=―――――――=―――=――
(χの増加量) 4 1
(傾き)が−2 (切片)−2 になりますから、
y=−2χ−2 になります。
R座標のyは、P座標のyの座標(1/2a−2)になります。
残るのは、R座標のχになります。
y=−2χ−2 に1/2a−2 を代入します。
1/2a−2=−2χ−2
−2χ−2=1/2a−2
−4χ−4=a−4
−4χ=a−4+4
−4χ=a
χ=−1/4 a
になります。
これで、点Rの(χ、y)=(−1/4 a、1/2a−2)
答え χ=−1/4 a










コメント