中学3年数学 関数y=aχ² まとめテスト6・解答
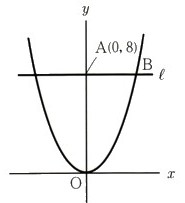
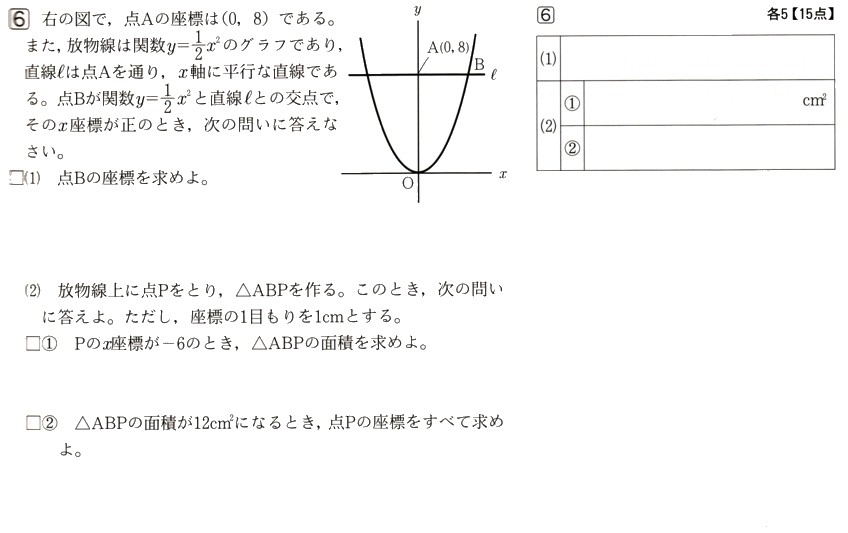
6、次の図 で、点Aの座標は(0,8)であるとき、また、放物線は関数y=1/2χ²のグラフであり、直線ℓは点Aを通り、χ軸に平行な直線になります。点Bが関数y=1/2χ²と直線ℓとの交点で、そのχ座標が正のとき、次の問いに答えてください。
で、点Aの座標は(0,8)であるとき、また、放物線は関数y=1/2χ²のグラフであり、直線ℓは点Aを通り、χ軸に平行な直線になります。点Bが関数y=1/2χ²と直線ℓとの交点で、そのχ座標が正のとき、次の問いに答えてください。
(1)点Bの座標を求めてください。
点Aの座標が(0,8)ですから、点Bのy座標は8になります。
y=1/2χ² の式にy=8 を代入します。
8=1/2(χ²)
χ²=8×2
χ²=16
χ=4
答え 点Bの座標(4、8)
(2)放物線上に点Pをとり、△ABPをつくります。このとき、次の問いに答えてください。ただし、1目盛りは?とします。
?Pのχ座標が−6のとき、△ABPの面積を求めてください。
Pのy座標を求めるためにy=1/2χ²にχ=−6を代入します。
y=1/2(−6²)
y=1/2(36)
y=18
点Pの座標は(−6,18)になります。
三角形の面積は底辺×高さ÷2ですから、
底辺をABとします。
ABの長さは4cm、
高さは(点Pのy座標)−(点Aのy座標)=18−8=10?
4×10÷2=20
△ABPの面積は20㎠
答え 20㎠
?△ABPの面積が12㎠になるとき、点Pの座標をすべて求めてください。
△ABPが12㎠になる点Pの位置が放物線y=1/2χ²上で底辺になるABより上になるか下になるかです。
上になる場合は?のときと同じようにして求めることができます。
下になるときは、4×{(点Aのy座標8) −(点Pのy座標)}÷2=12
で求めることができます。
まずは点Pが底辺ABより上にある場合。
底辺は?のときと同じですから4cmになります。
底辺×高さ÷2=12㎠
4 ×{ (点Pのy座標)−(点Aのy座標8)}÷2=12
2(p−8)=12
2p−16=12
2p=12+16
2p=28
p=14
点Pのy座標=14ですからy=1/2χ²の式にy=14を代入します。
14=1/2χ²
28=χ²
χ=±√28
2)28
2)14
7
χ=±2√7
次に、点Pが底辺ABより下にある場合。
4×{(点Aのy座標8) −(点Pのy座標)}÷2=12
2(8−p)=12
16−2p=12
−2p=12−16
−2p=−4
p=2
点Pのy座標がわかりましたからy=1/2χ²の式にy=2を代入します。
2=1/2χ²
4=χ²
χ=±2
これですべての座標がわかりました。
答え
(2√7、14)、(−2√7、14)、(2、2)、(−2、2)







コメント