中学2年数学 平面図形 三角形の性質 確認問題5・解答
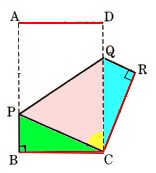
5、図 は、AB>BCである長方形ABCDの紙を、頂点Aが頂点Cに重なるように折り返したものになります。頂点Dが移った点をR、折り目をPQとするとき、次の問いに答えてください。
は、AB>BCである長方形ABCDの紙を、頂点Aが頂点Cに重なるように折り返したものになります。頂点Dが移った点をR、折り目をPQとするとき、次の問いに答えてください。
 は、AB>BCである長方形ABCDの紙を、頂点Aが頂点Cに重なるように折り返したものになります。頂点Dが移った点をR、折り目をPQとするとき、次の問いに答えてください。
は、AB>BCである長方形ABCDの紙を、頂点Aが頂点Cに重なるように折り返したものになります。頂点Dが移った点をR、折り目をPQとするとき、次の問いに答えてください。(1)△PBC≡△QRCであることを証明してください。
答え
〔証明〕
△PBCと△QRCにおいて、
□ABCDは長方形ですから、AD//BCになります。
それにより、AD=BC・・・①
CRは、折る前はADですから、
AD=CR・・・②
よってBC=CR・・・③
仮定により
∠PBC=90°
∠QRC=90°
∠PBC=∠QRC・・・④
∠PCBは、∠DCB(90°)から∠QCPを引いた角度になります。
∠PCB=90°ー∠QCP
∠QCRは、∠RCP(90°)から∠QCPを引いた角度になります。
(∠QCPは折る前は∠PAD)
∠QCR=90°ー∠QCP
よって、
∠PCB=∠QCR・・・⑤
③,④,⑤より
1つの辺とその両端の角がそれぞれ等しくなりますから
△PBC≡△QRC
になります。
(2) ∠PCB=40°のとき、∠PQRの大きさは何度になりますか?求めてください。
∠PCB=40°のとき、∠PQRの大きさは何度になりますか?求めてください。
 ∠PCB=40°のとき、∠PQRの大きさは何度になりますか?求めてください。
∠PCB=40°のとき、∠PQRの大きさは何度になりますか?求めてください。 まずは、△PBCについて考えます。
∠PCB=40°で、∠PBC=90°ですから、
∠APCは、∠PBCと∠PCBの外角になりますから、
∠APC=∠PBC+∠PCB
=90°+40°
=130°
PQは、∠APCの二等分線になりますから2で割れば、∠








コメント