中学2年数学 平面図形 三角形の性質 確認問題7・解答
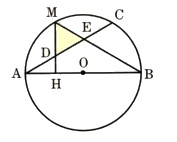
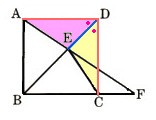
7、正方形ABCDの対角線BD上に点Eをとり、直線AEがBCの延長と交わる点をFとします。このとき、∠EFC=∠ECDであることを証明してください。
この問題は少しややこしくなります。
やり方としては、まず、△EFCと△ECDをいきなり考えるのではなくて、

△ECDと△EDAを証明して
∠ECD=∠EAD

だから、
∠EAD=∠EFC
と考えます。
それでは証明していきましょう。
答え
△ECDと△EDAにおいて

仮定により
正方形ですから4つの辺がそれぞれ等しくなります。
よって、
DA=DC・・・①
DE共通・・・②
BDは∠D(90°)の対角線ですから二等分線(45°)になります。
よって、
∠ADE=∠CDE・・・③
①.②.③より
2辺とその間の角がそれぞれ等しくなりますから
△ECD≡△EDA
になります。
合同な三角形の対応する角はそれぞれ等しくなりますから
∠ECD=∠EAD
になります。
つぎに、仮定により
ABCDの四角形は正方形ですから
AD//BCになります。
直線AFは平行な2つの線に交わる直線になりますから
錯角により

∠EAD=∠EFC
になります。

△ADE≡△CDE
ですから
∠EAD=∠ECD
よって、
∠ECD=∠EFC
になります。








コメント