中学3年数学　図形と相似　平行線と線分の比　確認問題１・解答

中学3年数学　図形と相似　平行線と線分の比　確認問題１・解答

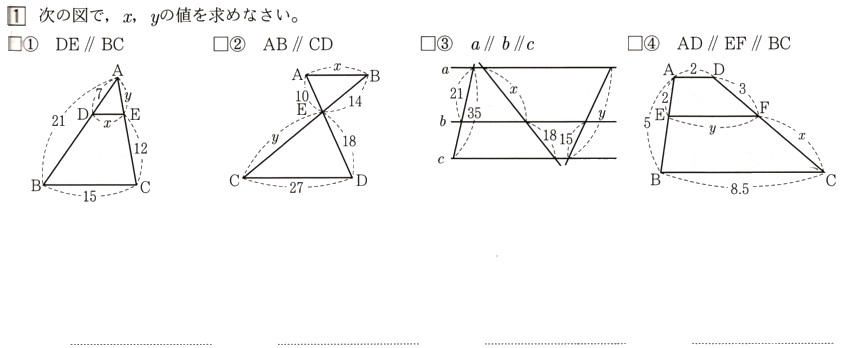
１、次の図で、χ、ｙの値を求めてください。

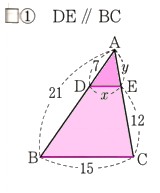
?,△ＡＤＥと△ＡＢＣで考えます。

ＡＤ：ＡＢ＝ＤＥ：ＢＣ

ＡＤ＝７

ＡＢ＝２１

ＢＣ＝１５

ですから、ＤＥは

７：２１＝χ：１５

7×１５＝２１×χ

１０５＝２１χ

χ＝105/21

χ＝５

ＡＤ：ＡＢ＝１：３

ですから

ＡＥ：ＥＣ＝１：２

になります。

ＥＣ＝１２ ですから

ＡＥ：１２＝１：２

２×ｙ＝１×１２

２ｙ＝１２

ｙ＝１２/２

ｙ＝６

答え　　χ＝５、ｙ＝６

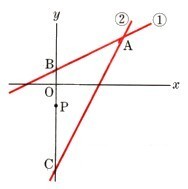
?,△ＡＥＢと△ＤＥＣで考えます。

ＡＥ：ＥＤ＝ＢＥ：ＣＥ

ＡＥ＝１０

ＥＤ＝１８

ＢＥ＝１４

ですから、

１０：１８＝１４：ｙ

１０×ｙ＝１８×１４

１０ｙ＝２５２

ｙ＝25.2

ＡＥ：ＥＤ＝５：９

ですから

ＡＢ：ＣＤ＝５：９

ＣＤ＝２７

ですから

χ：２７＝５：９

χ×９＝27×５

9χ＝１３５

χ＝１５

答え　　χ＝１５、ｙ＝25.2

?,まずは、ｂｃを考えます。

ａｂ：ａｃ＝２１：３５＝３：５

ですから、ａｂ：ｂｃ＝３：２

になります。

これにより、χ：１８＝３：２

χ×２＝18×３

2χ＝５４

χ＝２７

ｙは、15：ｙ＝２：５

１５×5＝ｙ×２

２ｙ＝７５

ｙ＝37.5

答え　　χ＝２７、ｙ＝37.5

?,ＡＥ：ＡＢ＝２：５

ＡＥ：ＥＢ＝２：３

ＡＥ：ＥＢ＝ＤＦ：ＦＣ＝２：３

３：χ＝２：３

３×３＝χ×２

２χ＝９

χ＝９/２

χ＝4.5

次に、ｙを考えます、

そのために、補助線をＤＣに平行な線をＡから引きます。

そして、△ＡＥＧと△ＡＢＨで考えます。

そうすると、ＡＥ：ＡＢ＝ＥＧ：ＢＨ

ＡＥ：ＡＢ＝２：５ですから

ＥＧ：ＢＨ＝２：５になります。

ＢＨ＝ＢＣ−ＨＣ

6.5＝8.5−２

ＥＧ：6.5＝２：５

ＥＧ×５＝6.5×２

５ＥＧ＝１３

ＥＧ＝13/5

ＥＧ＝2.6

ｙ＝ＥＧ＋ＧＦ

ＧＦ＝２

ＥＧ＝2.6

ｙ＝2＋2.6

ｙ＝4.6

答え　　χ＝4.5、ｙ＝4.6