中学３年数学　三平方の定理の利用　確認問題３・解答

中学３年数学　三平方の定理の利用　確認問題３・解答

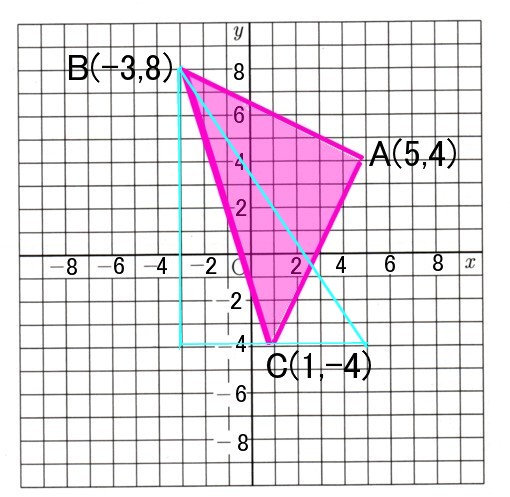
３、１目盛りを１ｃｍとする座標平面上に、３点Ａ（５、４）Ｂ（−３、８）Ｃ（１、−４）があるとき、

次の問いに答えてください。

（１）ＡＢ，ＢＣ，ＣＡの長さを求めてください。

公式を利用して解いてみましょう。

ＡＢ＝√（χ₂−χ₁）²＋（ｙ₂−ｙ₂）²

Ａ（５、４） Ｂ（−３、８）

ＡＢ＝√（χ₂−χ₁）²＋（ｙ₂−ｙ₂）²

ＡＢ＝√（−３−５）²＋（８−４）²

ＡＢ＝√（−８）²＋（４）²

ＡＢ＝√６４＋１６

ＡＢ＝√８０

2)80
2)40
2)20
2)10
   5

ＡＢ＝４√５

答え　ＡＢ＝４√５?

Ｂ（−３、８） Ｃ（１、−４）

ＢＣ＝√（χ₂−χ₁）²＋（ｙ₂−ｙ₂）²

ＢＣ＝√（１−（−３））²＋（−４−８）²

ＢＣ＝√（４）²＋（−１２）²

ＢＣ＝√１６＋１４４

ＢＣ＝√１６０

2)160
2) 80
2) 40
2) 20
2) 10
     5
ＢＣ＝４√１０

答え　ＢＣ＝４√１０?

Ｃ（１、−４） Ａ（５、４）

ＣＡ＝√（χ₂−χ₁）²＋（ｙ₂−ｙ₂）²

ＣＡ＝√（５−１）²＋（４−（−４））²

ＣＡ＝√（４）²＋（８）²

ＣＡ＝√１６＋６４

ＣＡ＝√８０

ＣＡ＝４√５

答え　４√５?

（２）△ＡＢＣの面積を求めてください。

この三角形は２つの辺の長さが同じになりますから、二等辺三角形であることがわかります。

つぎに、この三角形が直角三角形か調べます。

三平方の定理が成り立てば直角だということがわかります。

辺ＡＢ＝辺ＡＣ

４√５?＝４√５?

辺ＢＣ＝４√１０?

（ＡＢ）²＋（ＡＣ）²＝（ＢＣ）²

（４√５）²＋（４√５）²＝（４√１０）²

８０＋８０＝１６０

（４√１０）²＝１６０

式が成り立ちますからこの三角形は直角二等辺三角形ということがわかりました。

次に直角二等辺三角形で考えます。

斜辺を４√５で考え、その他の１辺をχとします。

直角二等辺三角形の辺の比率は

（１辺）：（１辺）：（斜辺）＝１：１：√２

χ：４√５＝１：√２

χ×√２＝４√５×１

χ√２＝４√５

χ＝４√５／√２

χ＝４√５×√２／√２×√２

χ＝４√１０／２

χ＝２√１０

三角形の面積は底辺×高さ÷２

底辺は４√１０?、高さは２√１０?

４√１０×２√１０÷２

＝８０÷２＝４０

答え　　４０㎠