中学3年数学　三平方の定理　確認問題４・解答

中学3年数学　三平方の定理　確認問題４・解答

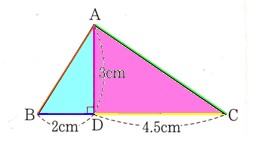
４、次の図の△ＡＢＣで、ＡからＢＣに垂線ＡＤを引きます。

ＡＤ＝3ｃｍ、ＢＤ＝2ｃｍ、ＣＤ＝4.5? になります。

次の問いに答えてください。

（１）ＡＢの長さを求めてください。

△ＡＢＤで考えます。

△ＡＢＤは直角三角形ですから、三平方の定理を利用します。

辺ＡＢの長さをχとして考えます。

辺ＢＤ＝２?

辺ＡＤ＝３?

（ＢＤ）²＋（ＡＤ）²＝（ＡＢ）²

２²＋３²＝χ²

４＋９＝χ²

χ²＝１３

χ＝±√１３?（χは＋ですから）

χ＝√13?

答え　√13?

（２）△ＡＢＣは直角三角形であることを、三平方の定理を使って証明してください。

三平方の定理は、

ａ²＋ｂ²＝ｃ²（ａ、ｂは直角を挟む2つの辺。ｃは斜辺。）

ならば、直角三角形ということになります。

  答え

斜辺は辺ＢＣ＝２＋4.5＝6.5?

辺ＡＢは、（１）で√13?とわかりました。

辺ＡＣは△ＡＤＣで考えます。

（辺ＡＤ）²＋（辺ＤＣ）²＝（辺ＡＣ）²

辺ＡＤ＝３cm

辺ＤＣ＝4.5?

辺ＡＣ＝χ?とします。

３²＋（4.5）²＝χ²

９＋20.25＝29.25

χ²＝29.25

χ＝±√29.25（χは＋になります。）

χ＝√29.25

辺ＡＣの長さが√29.25とわかりました。

3つの辺がそれぞれわかりましたから、三平方の定理にあてはめてみます。

（ＡＢ）²＋（ＡＣ）²＝（ＢＣ）²

ＡＢ＝√13?

ＡＣ＝√29.25?

ＢＣ＝6.5?

（√13）²＋（√29.25）²＝１３＋29.25＝42.25

（6.5）²＝42.25

三平方の定理の式が成り立ちますから。△ＡＢＣは直角三角形ということがわかります。