中学３年数学　三平方の定理の利用　確認問題１・解答

中学３年数学　三平方の定理の利用　確認問題１・解答

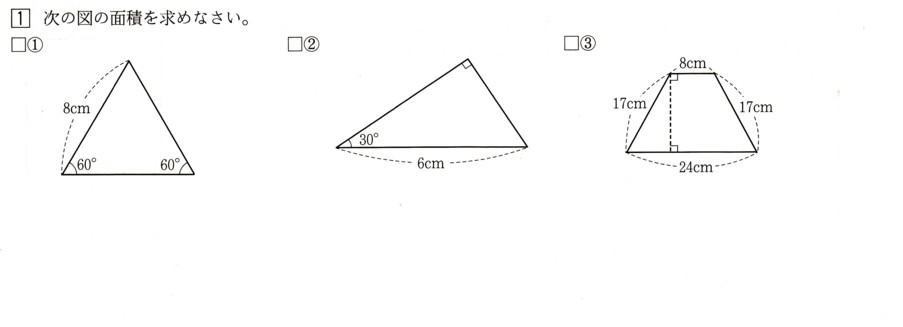
１、次の図の面積を求めてください。

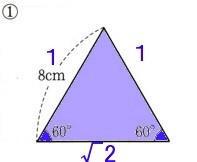
?、１辺が８ｃｍの正三角形になります、

高さがわかれば面積はわかりますから、高さを考えていきます。

６０゜の角を持つ直角三角形の比は（底辺）：（斜辺）：（高さ）＝１：２：√３

高さをχとして考えます。

（斜辺）：（高さ）＝２：√３＝８：χ

２：√３＝８：χ

２×χ＝８×√３

２χ＝８√３

χ＝４√３

高さが４√３とわかりました。

三角形の面積は

底辺×高さ÷２＝８cm×４√３cm÷２

＝１６√３㎠

答え　１６√３㎠

?、この図形も６０゜の角を持つ直角三角形になりますから、

比は（底辺）：（斜辺）：（高さ）＝１：２：√３

斜辺が６ｃｍですから、底辺は３cmになります。

高さはχとして考えます。

２：√３＝６：χ

２×χ＝６×√３

２χ＝６√３

χ＝３√３

高さが３√３?とわかりました。

三角形の面積は

底辺×高さ÷２＝３?×３√３?÷２

＝９√３/２㎠

答え　９√３／２㎠

?、台形の面積は（上底＋下底）×高さ÷２ですから、

上底＝８ｃｍ

下底＝２４?

高さ＝χ?

高さを求めるために、台形の面積から１辺が８ｃｍ四角形の面積を引いて考えます。

１７?が斜辺になり、この三角形の底辺は、

２４−８＝１６?になります。

直角三角形で考えると。

斜辺は１７?、底辺は８cmとなります。

三平方の定理を使い考えます。

８²＋χ²＝１７²

６４＋χ²＝２８９

χ²＝２８９−６４

χ²＝２２５

χ＝１５（χは＋ですから）

χ＝１５ｃｍになります。

上底＝８ｃｍ

下底＝２４?

高さ＝１５?

（８＋２４）×１５÷２

＝