中学２年数学　平面図形　平行四辺形の性質　確認問題７・解答

中学２年数学　平面図形　平行四辺形の性質　確認問題７・解答

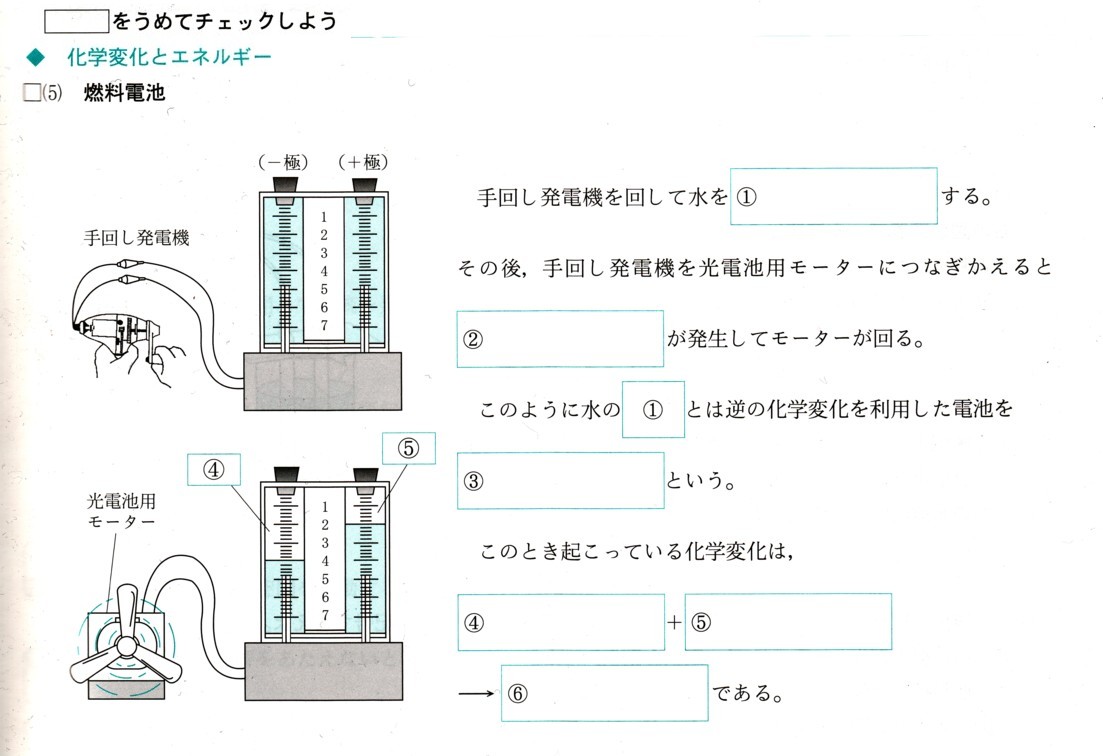
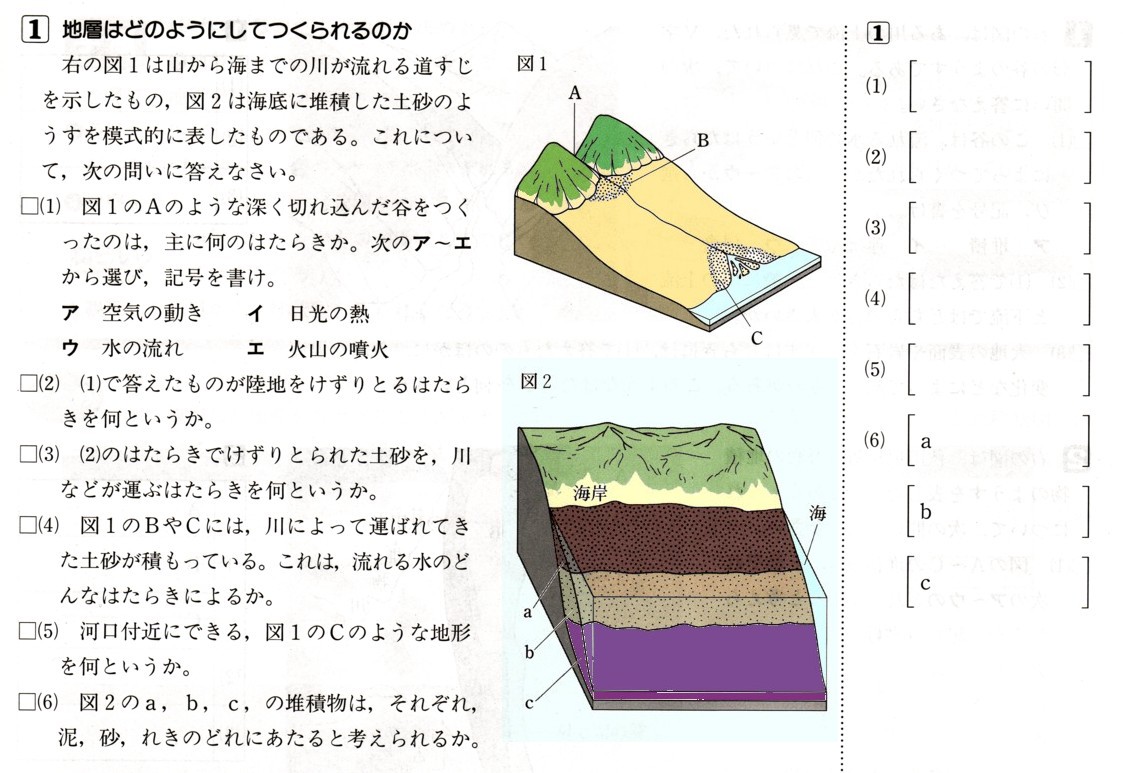
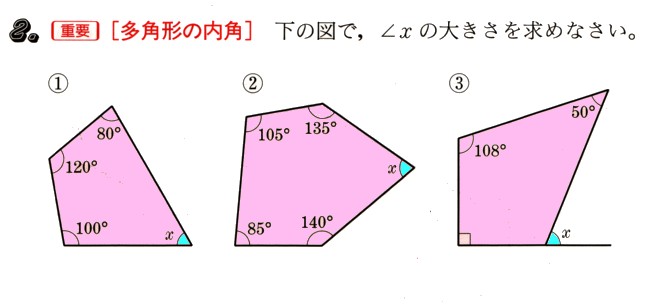
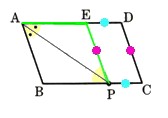
７、平行四辺形ＡＢＣＤの∠Ａの二等分線と辺ＢＣとの交点をＰとするとき、ＰＣ＋ＣＤ＝ＡＤであることを証明してください。

答え

〔証明〕

補助線を点ＰからＣＤに平行な直線を引きＡＤに接する点をＥとします。

これにより四角形ＥＰＣＤは平行四辺形になります。

平行四辺形は向かい合う２つの辺の長さはそれぞれ等しくなりますから、

ＥＤ＝ＰＣ・・・①

ＥＰ＝ＣＤ・・・②

次に、△ＡＢＣと△ＡＥＰにおいて

仮定より

∠ＢＡＰ＝∠ＥＡＰ・・・③

ＡＥ//ＢＰですから

錯角により

∠ＥＡＰ＝∠ＢＰＡ・・・④

ＡＢ//ＥＰですから

錯角により

∠ＢＡＰ＝∠ＥＰＡ・・・⑤

∠ＢＡＰ＝∠ＥＡＰですから

∠ＥＡＰ＝∠ＥＰＡ・・・⑥

になります。

２つの角がそれぞれ等しくなりますから

△ＥＡＰは二等辺三角形になります

二等辺三角形は頂角を挟む２つの辺の長さは等しくなりますから

ＡＥ＝ＰＥ・・・⑦

ＥＰ＝ＣＤ・・・②

ＡＥ＝ＣＤ・・・⑧

ＡＤ＝ＡＥ＋ＥＤ

②、⑧より

ＡＤ＝ＰＣ＋ＣＤ

になります。