中学3年数学 三平方の定理の利用 3確認問題1・解答
1、次の問いに答えてください。
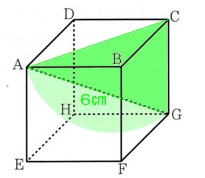
(1)図 のように、点A,B,C,D,E,F,G,Hを頂点とする立方体があります。
のように、点A,B,C,D,E,F,G,Hを頂点とする立方体があります。
この立方体の対角線AGの長さが6?のとき、立方体の体積を求めてください。
立方体の対角線を求める式で考えます。
(立方体の対角線)=√(縦)²+(横)²+(高さ)²
(立方体の対角線)=6?
立方体ですから縦、横、高さの長さはすべて等しくなります。
√χ²+χ²+χ²=√3χ²=χ√3
6=χ√3
χ=6/√3
χ=6√3/√3×√3
χ=6√3/3
χ=2√3
1辺の長さが2√3?とわかりました。
立方体の体積は(縦)×(横)×(高さ)
2√3×2√3×2√3=24√3㎤
答え 24√3㎤
(2)次の図 は、高さ12?、底面の半径5?の円錐になります。この円錐の側面積を求めてください。
は、高さ12?、底面の半径5?の円錐になります。この円錐の側面積を求めてください。
側面積を求めるために、まずは、OAの長さを求めます。
△OHAを三平方の定理を利用して考えます。
(底辺)²+(高さ)²=(斜辺)²
AH=5?
OH=12?
OA=χ?として考えます。
5²+12²=χ²
25+144=χ²
169=χ²
χ=13(χは+になります)
OA=13?
次に、側面の面積=扇形の面積を考えます。
OAの長さはOを中心にした扇形の半径の長さになります。
扇形の面積は(半径)²×π×扇形の内角/360゜
半径は13?
扇形の内角は(底面の円周)/(扇形の半径の円周)×360゜
底面の円周=2×5×π=10π?
扇形の中心角をaとして考えます。
扇形の周の長さは、2×(半径)×π×a/360゜
扇形の半径は13?
2×13×π×a/360゜
=26πa/360
(底面の円周)=(扇形の周の長さ)
10π?=26πa/360?
a/360=10/26
a/360=5/13
扇形の面積=(半径)²×π×(中心角)
半径=13?
中心角=5/13゜
(13)²π×5/13=169×5π/13
=13×5π
=65π㎠
答え 65π„
16;










コメント