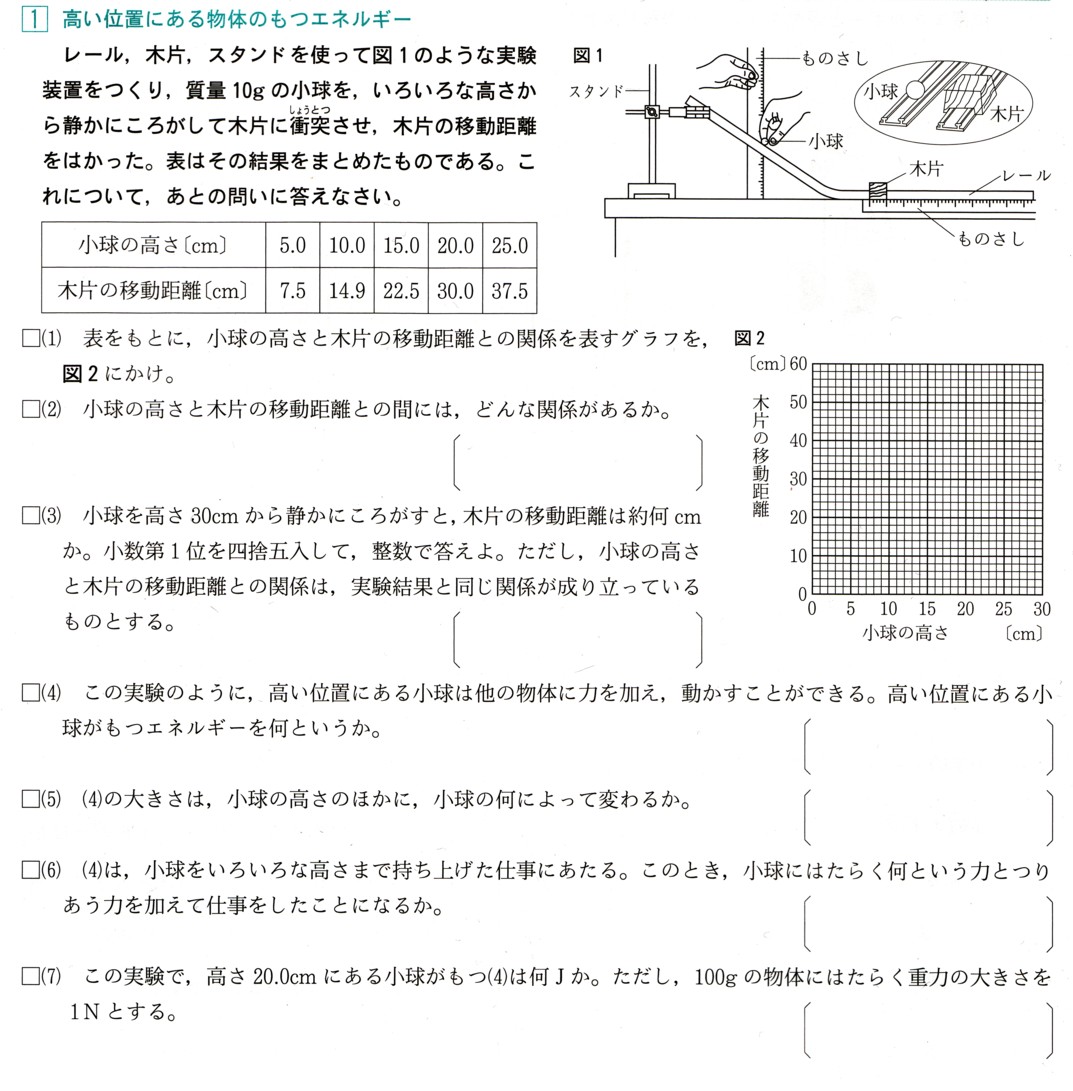
中学1年数学 円とおうぎ形2 練習問題4 解答・解説
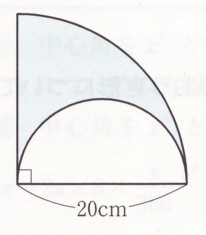
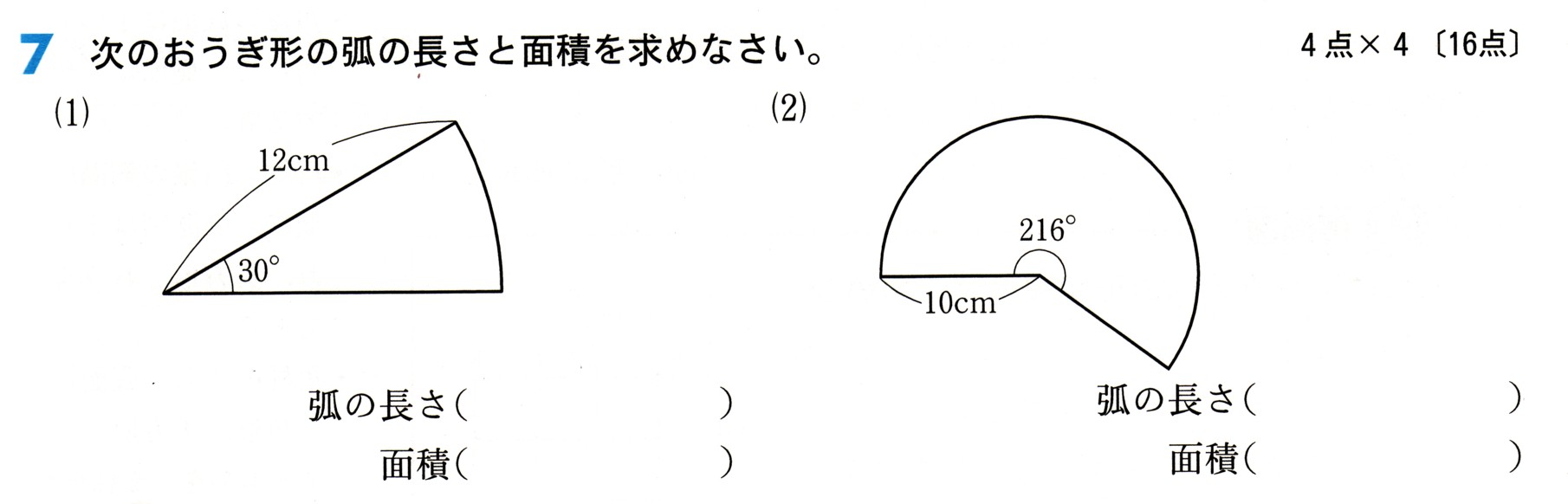
次の図は、それぞれおうぎ形と半円を組み合わせてできた図形です。色を塗った
部分の周の長さと面積を求めてください。
この場合は、まず2つの図形を組み合わせたときの。面積を求めます。
その求めた面積から直径20cmの半円の面積をひけば、色のついた図形の
面積がわかります。
それでは考えていきましょう
組み合わせた図形の形は、
半径20cmの円の1/4のおうぎ形ということがわかりす。
この扇形の面積の求め方は、
S=πγ²×1/4
(おうぎ形の面積)=半径×半径×π×1/4
=20×20×π×1/4
=100π
つぎに、直径20cmの半円の面積を求めます
式は、S=πγ²×1/2
になりますから
(半円の面積)=半径×半径×π×1/2
=10×10×π×1/2
=50π
(おうぎ形の面積)−(半円の面積)すれば、色のついた図形の面積がわかります
100π−50π=50π
色のついた図形の面積は、50πc?
次に、色のついた図形の周を考えます
まずは、色のついた図形の弧の長さは、大きい図形の弧の長さですから、
この弧の長さに、大きいおうぎ形の半径の長さと、半円の弧の長さを加えれば
、色のついた図形の周の長さが
わかります。
それでは考えていきましょう
弧の長さを求める式は
ℓ=2πγ×中心角/360
わかっているのは、半径20cm、中心角90゜
(大きいおうぎ形の弧の長さ)=2π×半径×中心角/360
=2π×20×90/360
=10π
そして、大きいおうぎ形の半径を加えます
半径は20cmですから
10π+20(cm)
次に半円の弧の長さを求めます
弧の長さの式は、同じです
ℓ=2πγ×中心角/360
わかっているのは、半径10cm、中心角180゜
(半円の弧の長さ)=2π×半径×中心角/360
=2π×10×180/360
=10π
これで、すべての長さがわかりました。
(おうぎ形の弧の長さ)+(おうぎ形の半径)+(半円の弧の長さ)=
色のついた図形の周
10π+20+10π=20π+20(cm)
答え 周の長さ 20π+20(cm) 、面積 50πc?
今回は、2つの図形をあわせた面積から小さいおうぎ形の面積をひけば、
色のついた図形の面積がわかります。
それでは考えていきましょう。
大きいおうぎ形の面積の式は、
S=πγ²×中心角/360
(おうぎ形の面積)=半径×半径×π×中心角/360
わかっているのは半径 20cm
中心角 108゜
それでは、式にあてはめていきます
(おうぎ形の面積)=20×20×π×108/360
=120π
つぎに、小さいおうぎ形の面積を求めます
式は同じです
(おうぎ形の面積)=半径×半径×π×中心角/360
わかっているのは半径 10cm
中心角 108゜
(おうぎ形の面積)=10×10×π×108/360
=30π
(大きいおうぎ形の面積)−(小さいおうぎ形の面積)=色のついた図形の面積
120π − 30π = 90π
面積がわかりました
次に周の長さを考えていいます。
周の求め方は、大きいおうぎ形の弧の長さと小さいおうぎ形の弧の長さと
大きいおうぎ形の半径から、小さいおうぎ形の半径をひいた長さ。
になります。
まずは、大きいおうぎ形の弧を求めます。
おうぎ形の弧を求める式は、
ℓ=2πγ×中心角/360
(大きいおうぎ形の弧の長さ)=2π×半径×中心角/360
わかっているのは、
半径20cm
中心角 108゜
あてはめていきます
(大きいおうぎ形の弧の長さ)=2π×20×108/360
=40π×3/10
=12π
次に小さいおうぎ形の弧の長さを求めます。
(小さいおうぎ形の弧の長さ)=2π×半径×中心角/360
わかっているのは、
半径10cm
中心角 108゜
あてはめていきます
(小さいおうぎ形の弧の長さ)=2π×10×108/360
=20π×3/10
=6π
残りの周は、20cm−10cm が2つありますから。
(20cm−10cm)×2=20cm
すべてをたします。
(大きいおうぎ形の弧の長さ)+(小さいおうぎ形の弧の長さ)+(残りの周)
12πcm + 6πcm + 20cm
色のついた図形の周の長さ=12π+6π+20
=18π+20cm
答え 面積 90πcm² 周の長さ 18π+20cm

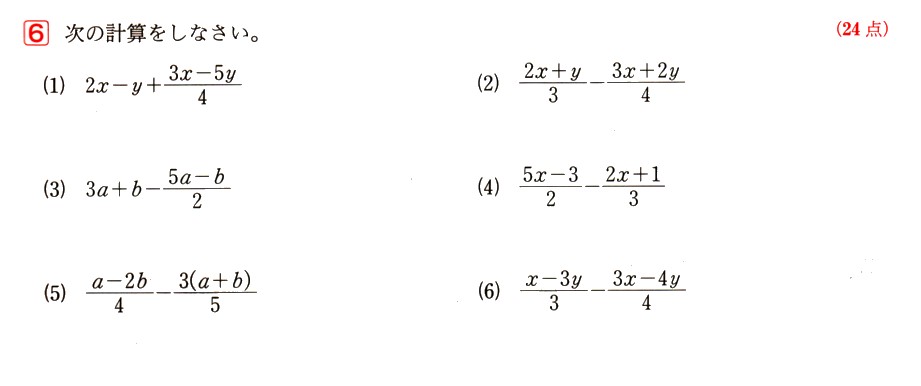









コメント