中学1年数学　立体の表面積と体積　確認問題2　解答・解説

中学1年数学　立体の表面積と体積　確認問題2　解答・解説

  　図のように底面の半径が4cmの円錐を、水平な平面上におき、頂点

　Ｏを中心として転がしたところ、最初の位置に戻るまでに、ちょうど

　3回転し、点線で示した円の上を１周しました。次の問いに答えてく

　ださい。

（１）この円錐の母線の長さを求めてください。

　　　三角錐の母線の長さは、水平面上を転がってできた円の半径

　　　になります。

　　　(三角錐の母線の長さ)＝(水平面上にできた円の半径)

　　(水平面上にできた円の半径)を求めるためには、円周の式を使えばわかります。

　　円周を求める式は、

　　(円周)＝2πγ

　　水平面の円周は、(円錐を3回転した長さになりますから)円錐の底面の円周の

　　長さがわかれば、水平面の円周がわかります。

　　3×(円錐の底面の円周)＝(水平面の円周)

　　　(円錐の底面の円周)を求める式は、

　　(円錐の底面の円周)＝2πγ

　　　　　　　　　　　＝2×半径×π

　　　　半径は4cmですから、

　　　　　　　　　　　＝2×4×π

　　　　　　　　　　　＝8π?

　　　3×(円錐の底面の円周)＝(水平面の円周)　ですから

　　　3×8πcm＝(水平面の円周)　

　　　　24πcm＝(水平面の円周)　になります。

　　(水平面の円周)　が24πcmとわかりましたから、

　　円周を求める式から、半径を求めます。

　　(円周)＝2×(半径)×π

　　24πcm＝2×(半径)×π

　　　両辺に1/2πをかけます

　　1/2π×24πcm＝1/2π×2×(半径)×π

　　　12cm＝(半径)

　　水平面の円の半径がわかりました。

　　(水平面の円の半径)＝(円錐の母線の長さ)

　　になりますから

　　(円錐の母線の長さ)＝12cm

　　　　答え　　12cm

（２）この円錐の表面積を求めてください。

　　円錐の表面積を求める式は

　　　(円錐の表面積)＝(底面積)＋(側面積)

　　　　　　　　　　＝(円の面積)＋(おうぎ形の面積)

　　　になります。

　　　　(円の面積)＝πγ²
　　
　　　　底面の半径は4cm

　　　　　　　　　＝4×4×π

　　　　　　　　　＝16π?²

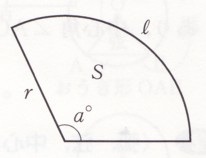
　　　　(おうぎ形の面積)＝πγ²×中心角/360

　　　半径は、母線の長さ12cmですが、中心角がまだわかりません。

　　　　中心角を求めるために、

　　おうぎ形の弧の長さと、円錐の底面の円周の長さは等しいのですから

　　中心角をχとし方程式を使って求めていきます。

　　(おうぎ形の弧の長さ)＝(底面の円周の長さ)

　　それぞれの式で考えます

　　(おうぎ形の弧の長さ)＝2πγ×中心角/360

　　(底面の円周の長さ)＝2πγ

　　(2πγ×中心角/360)＝(2πγ)

　　(2×半径×π×中心角/360)＝(2×半径×π)

　　おうぎ形の条件は、半径＝円錐の母線の長さ＝12cm

　　　　　　　　　　　　中心角はχ゜とします。

　　底面の円の条件は、半径＝4cm

　　(2×12×π×χ/360)＝(2×4×π)

　　24π×χ/360＝8π

　　両辺に360をかけます

　　24πχ＝360×8π

　　両辺に1/24πをかけます

　　1/24π×24πχ＝1/24π×360×8π

　　　　　　χ＝120

　　　おうぎ形の中心角が120゜とわかりました。

　　弧の中心角を、おうぎ形の面積を求める式にあてはめます。

　　　(おうぎ形の面積)＝πγ²×中心角/360

　　　半径12cm、中心角120゜

　　　　(おうぎ形の面積)＝(半径)×(半径)×π×中心角/360

　　　　　　　　　　　　＝12cm×12cm×π×120/360