中学1年数学 円とおうぎ形 確認問題3 解答・解説
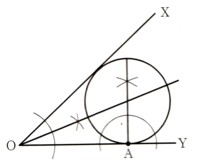
図のように、∠XOYと線分OY上の点Aがあるとき、中心が∠XOYの
二等分線上にあり、線分OYと点Aで接する円を、定規とコンパスを用いて
作図してください。
まずは、∠Oの二等分線を作図しましょう。
点Oを中点にして、適当な円をかきます、その円と、辺OX、OYに接した
交点を中点にして、半径が等しい円をかきます。その2つの円の交点と、点O
を直線で結びます。その直線が∠Oの二等分線になります。
つぎに、点Aの垂線を引きます、この垂線が円の接線になります。
それでは点Aの垂線を作図していきましょう。
辺OYの点Aを中心に円をかきます。辺OYに接する2つの交点ができます。
その2つの交点を中心に、半径が等しい円をかきます。その2つの円の交点
と点Aを直線で結びます。
この点Aから伸びた直線と∠Oの二等分線の交点が円の中心になります。
この中点と点Aを半径ににした円を作図します。
答え 図







コメント